Maximum-likelihood Estimators in Physics-Informed Neural Networks for High-dimensional Inverse Problems

Physics-informed neural networks (PINNs) have proven a suitable mathematical scaffold for solving inverse ordinary (ODE) and partial differential equations (PDE). Typical inverse PINNs are formulated as soft-constrained multi-objective optimization problems with several hyperparameters. In this work, we demonstrate that inverse PINNs can be framed in terms of maximum-likelihood estimators (MLE) to allow explicit error propagation from interpolation to the physical model space through Taylor expansion, without the need of hyperparameter tuning. We explore its application to high-dimensional coupled ODEs constrained by differential algebraic equations that are common in transient chemical and biological kinetics. Furthermore, we show that singular-value decomposition (SVD) of the ODE coupling matrices (reaction stoichiometry matrix) provides reduced uncorrelated subspaces in which PINNs solutions can be represented and over which residuals can be projected. Finally, SVD bases serve as preconditioners for the inversion of covariance matrices in this hyperparameter-free robust application of MLE to ``kinetics-informed neural networks''.

Kinetics-Informed Neural Networks

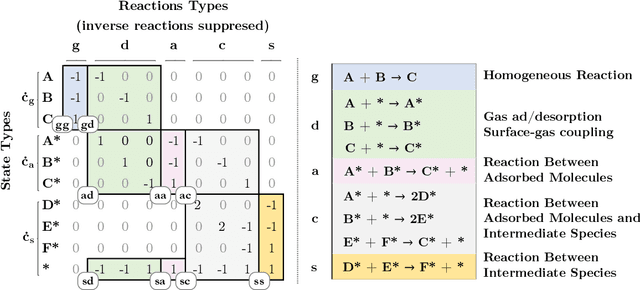
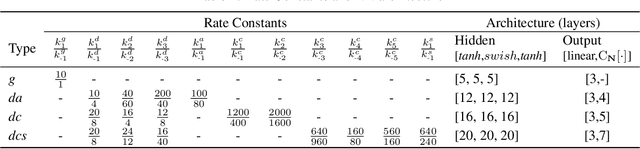
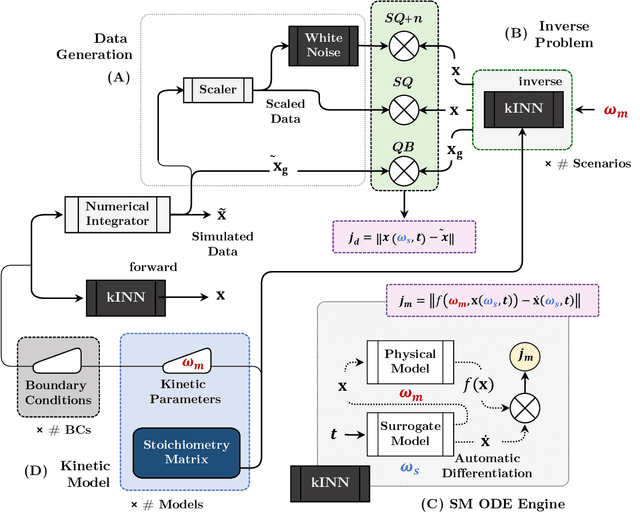
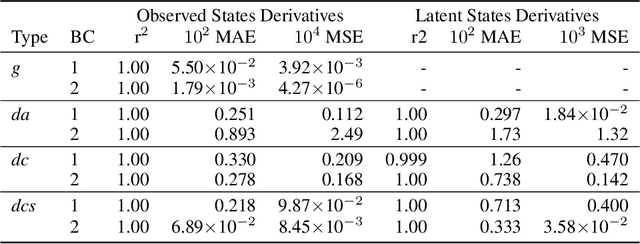
Chemical kinetics consists of the phenomenological framework for the disentanglement of reaction mechanisms, optimization of reaction performance and the rational design of chemical processes. Here, we utilize feed-forward artificial neural networks as basis functions for the construction of surrogate models to solve ordinary differential equations (ODEs) that describe microkinetic models (MKMs). We present an algebraic framework for the mathematical description and classification of reaction networks, types of elementary reaction, and chemical species. Under this framework, we demonstrate that the simultaneous training of neural nets and kinetic model parameters in a regularized multiobjective optimization setting leads to the solution of the inverse problem through the estimation of kinetic parameters from synthetic experimental data. We probe the limits at which kinetic parameters can be retrieved as a function of knowledge about the chemical system states over time, and assess the robustness of the methodology with respect to statistical noise. This surrogate approach to inverse kinetic ODEs can assist in the elucidation of reaction mechanisms based on transient data.