Kinetics-Informed Neural Networks

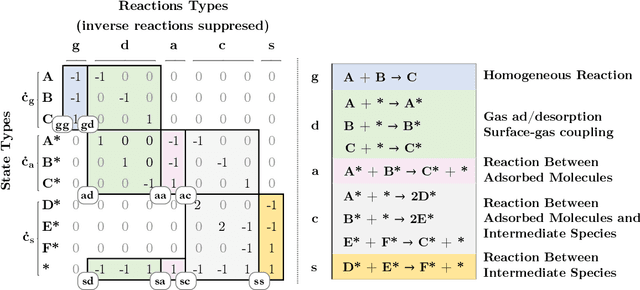
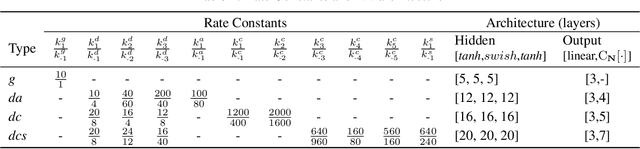
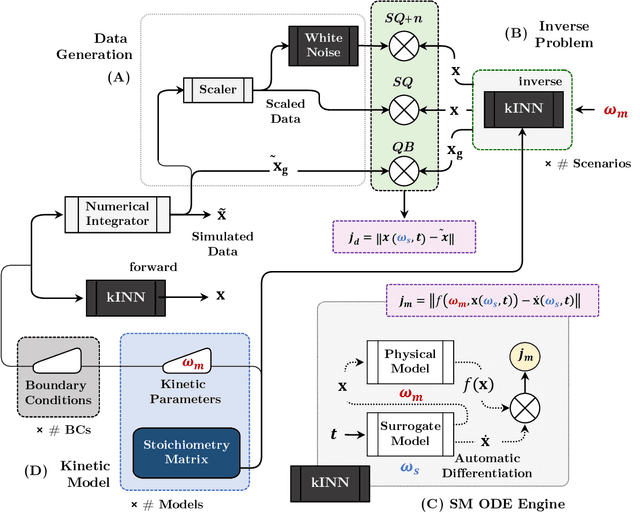
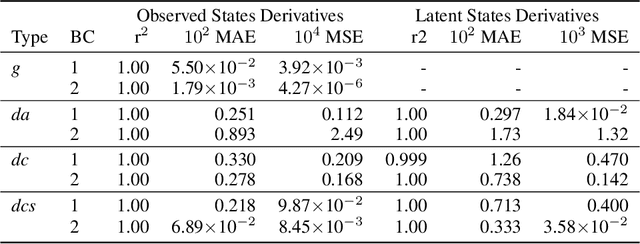
Chemical kinetics consists of the phenomenological framework for the disentanglement of reaction mechanisms, optimization of reaction performance and the rational design of chemical processes. Here, we utilize feed-forward artificial neural networks as basis functions for the construction of surrogate models to solve ordinary differential equations (ODEs) that describe microkinetic models (MKMs). We present an algebraic framework for the mathematical description and classification of reaction networks, types of elementary reaction, and chemical species. Under this framework, we demonstrate that the simultaneous training of neural nets and kinetic model parameters in a regularized multiobjective optimization setting leads to the solution of the inverse problem through the estimation of kinetic parameters from synthetic experimental data. We probe the limits at which kinetic parameters can be retrieved as a function of knowledge about the chemical system states over time, and assess the robustness of the methodology with respect to statistical noise. This surrogate approach to inverse kinetic ODEs can assist in the elucidation of reaction mechanisms based on transient data.