Sample size planning for conditional counterfactual mean estimation with a K-armed randomized experiment

We cover how to determine a sufficiently large sample size for a $K$-armed randomized experiment in order to estimate conditional counterfactual expectations in data-driven subgroups. The sub-groups can be output by any feature space partitioning algorithm, including as defined by binning users having similar predictive scores or as defined by a learned policy tree. After carefully specifying the inference target, a minimum confidence level, and a maximum margin of error, the key is to turn the original goal into a simultaneous inference problem where the recommended sample size to offset an increased possibility of estimation error is directly related to the number of inferences to be conducted. Given a fixed sample size budget, our result allows us to invert the question to one about the feasible number of treatment arms or partition complexity (e.g. number of decision tree leaves). Using policy trees to learn sub-groups, we evaluate our nominal guarantees on a large publicly-available randomized experiment test data set.

Neuroevolutionary Feature Representations for Causal Inference

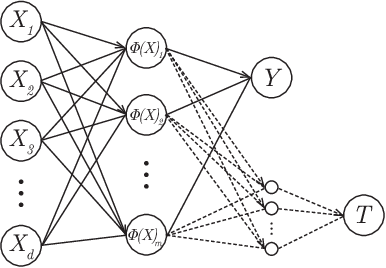
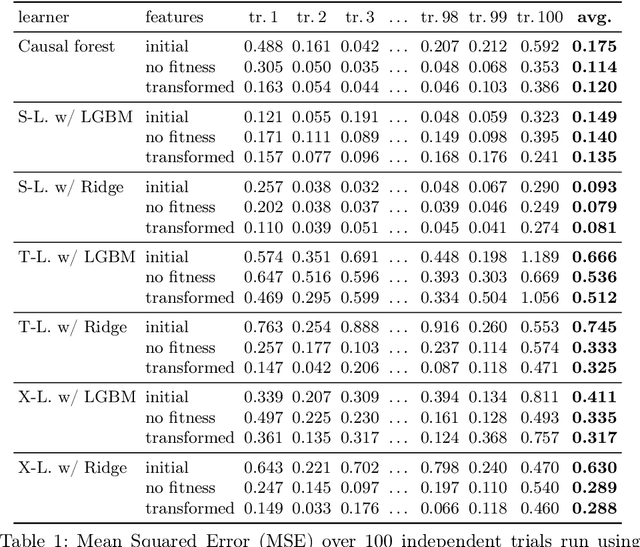
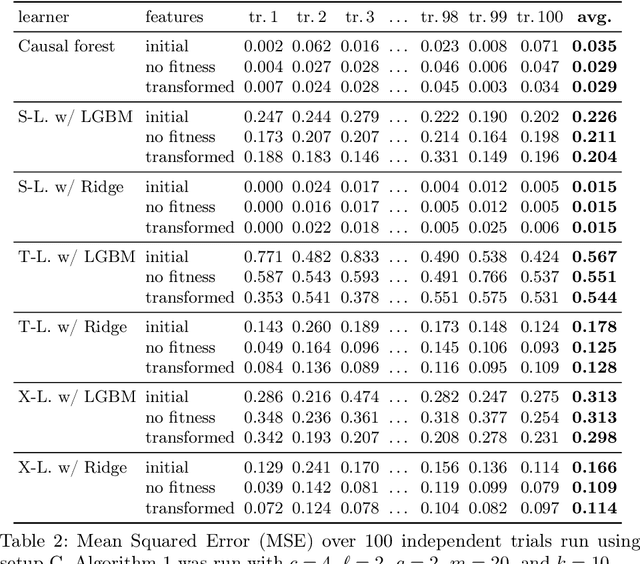
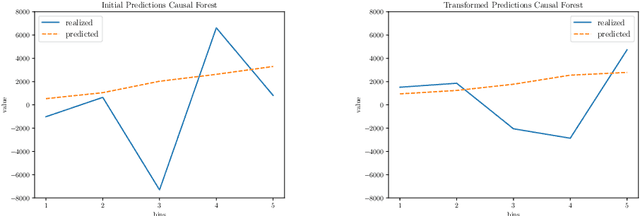
Within the field of causal inference, we consider the problem of estimating heterogeneous treatment effects from data. We propose and validate a novel approach for learning feature representations to aid the estimation of the conditional average treatment effect or CATE. Our method focuses on an intermediate layer in a neural network trained to predict the outcome from the features. In contrast to previous approaches that encourage the distribution of representations to be treatment-invariant, we leverage a genetic algorithm that optimizes over representations useful for predicting the outcome to select those less useful for predicting the treatment. This allows us to retain information within the features useful for predicting outcome even if that information may be related to treatment assignment. We validate our method on synthetic examples and illustrate its use on a real life dataset.

Sequential Learning of the Topological Ordering for the Linear Non-Gaussian Acyclic Model with Parametric Noise

Causal discovery, the learning of causality in a data mining scenario, has been of strong scientific and theoretical interest as a starting point to identify "what causes what?" Contingent on assumptions, it is sometimes possible to identify an exact causal Directed Acyclic Graph (DAG), as opposed to a Markov equivalence class of graphs that gives ambiguity of causal directions. The focus of this paper is on one such case: a linear structural equation model with non-Gaussian noise, a model known as the Linear Non-Gaussian Acyclic Model (LiNGAM). Given a specified parametric noise model, we develop a novel sequential approach to estimate the causal ordering of a DAG. At each step of the procedure, only simple likelihood ratio scores are calculated on regression residuals to decide the next node to append to the current partial ordering. Under mild assumptions, the population version of our procedure provably identifies a true ordering of the underlying causal DAG. We provide extensive numerical evidence to demonstrate that our sequential procedure is scalable to cases with possibly thousands of nodes and works well for high-dimensional data. We also conduct an application to a single-cell gene expression dataset to demonstrate our estimation procedure.