Gabriel Krummenacher
Scalable Adaptive Stochastic Optimization Using Random Projections
Nov 21, 2016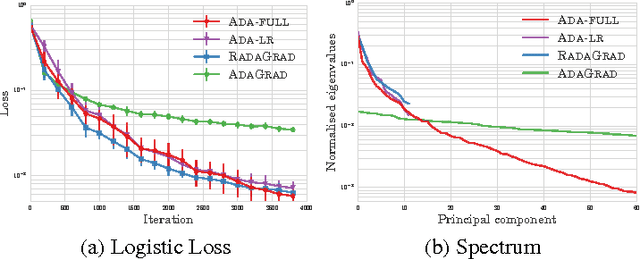
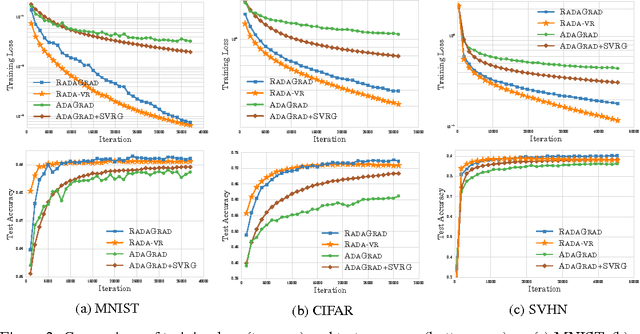
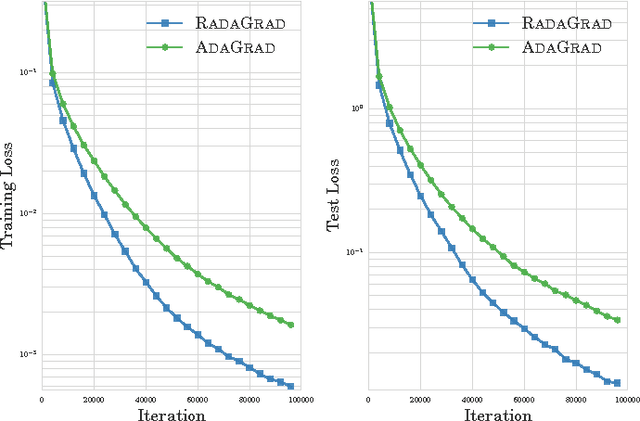
Abstract:Adaptive stochastic gradient methods such as AdaGrad have gained popularity in particular for training deep neural networks. The most commonly used and studied variant maintains a diagonal matrix approximation to second order information by accumulating past gradients which are used to tune the step size adaptively. In certain situations the full-matrix variant of AdaGrad is expected to attain better performance, however in high dimensions it is computationally impractical. We present Ada-LR and RadaGrad two computationally efficient approximations to full-matrix AdaGrad based on randomized dimensionality reduction. They are able to capture dependencies between features and achieve similar performance to full-matrix AdaGrad but at a much smaller computational cost. We show that the regret of Ada-LR is close to the regret of full-matrix AdaGrad which can have an up-to exponentially smaller dependence on the dimension than the diagonal variant. Empirically, we show that Ada-LR and RadaGrad perform similarly to full-matrix AdaGrad. On the task of training convolutional neural networks as well as recurrent neural networks, RadaGrad achieves faster convergence than diagonal AdaGrad.
LOCO: Distributing Ridge Regression with Random Projections
Jun 08, 2015
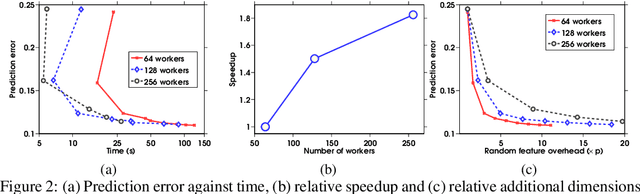

Abstract:We propose LOCO, an algorithm for large-scale ridge regression which distributes the features across workers on a cluster. Important dependencies between variables are preserved using structured random projections which are cheap to compute and must only be communicated once. We show that LOCO obtains a solution which is close to the exact ridge regression solution in the fixed design setting. We verify this experimentally in a simulation study as well as an application to climate prediction. Furthermore, we show that LOCO achieves significant speedups compared with a state-of-the-art distributed algorithm on a large-scale regression problem.
Fast and Robust Least Squares Estimation in Corrupted Linear Models
Jun 19, 2014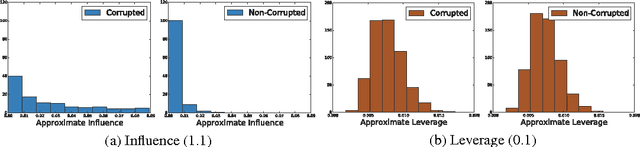
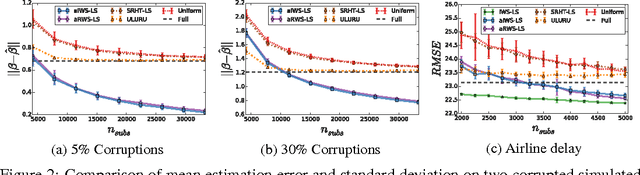
Abstract:Subsampling methods have been recently proposed to speed up least squares estimation in large scale settings. However, these algorithms are typically not robust to outliers or corruptions in the observed covariates. The concept of influence that was developed for regression diagnostics can be used to detect such corrupted observations as shown in this paper. This property of influence -- for which we also develop a randomized approximation -- motivates our proposed subsampling algorithm for large scale corrupted linear regression which limits the influence of data points since highly influential points contribute most to the residual error. Under a general model of corrupted observations, we show theoretically and empirically on a variety of simulated and real datasets that our algorithm improves over the current state-of-the-art approximation schemes for ordinary least squares.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge