Frederick Maier
Comparing Machine Learning Techniques for Alfalfa Biomass Yield Prediction
Oct 20, 2022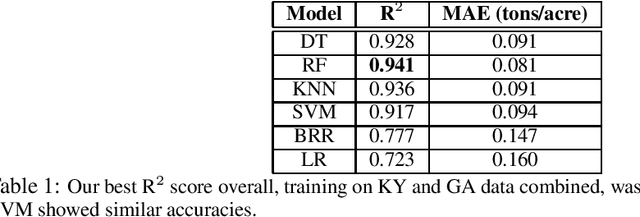
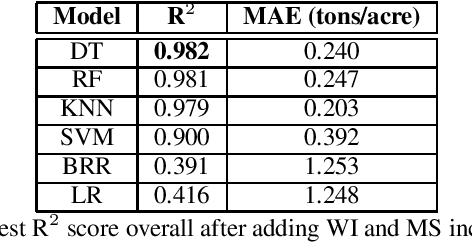
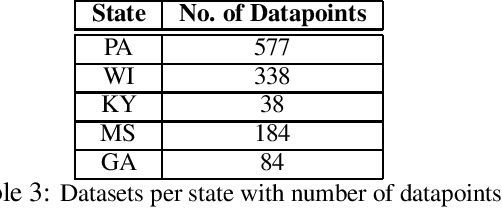
Abstract:The alfalfa crop is globally important as livestock feed, so highly efficient planting and harvesting could benefit many industries, especially as the global climate changes and traditional methods become less accurate. Recent work using machine learning (ML) to predict yields for alfalfa and other crops has shown promise. Previous efforts used remote sensing, weather, planting, and soil data to train machine learning models for yield prediction. However, while remote sensing works well, the models require large amounts of data and cannot make predictions until the harvesting season begins. Using weather and planting data from alfalfa variety trials in Kentucky and Georgia, our previous work compared feature selection techniques to find the best technique and best feature set. In this work, we trained a variety of machine learning models, using cross validation for hyperparameter optimization, to predict biomass yields, and we showed better accuracy than similar work that employed more complex techniques. Our best individual model was a random forest with a mean absolute error of 0.081 tons/acre and R{$^2$} of 0.941. Next, we expanded this dataset to include Wisconsin and Mississippi, and we repeated our experiments, obtaining a higher best R{$^2$} of 0.982 with a regression tree. We then isolated our testing datasets by state to explore this problem's eligibility for domain adaptation (DA), as we trained on multiple source states and tested on one target state. This Trivial DA (TDA) approach leaves plenty of room for improvement through exploring more complex DA techniques in forthcoming work.
Interdefinability of defeasible logic and logic programming under the well-founded semantics
Jun 10, 2011Abstract:We provide a method of translating theories of Nute's defeasible logic into logic programs, and a corresponding translation in the opposite direction. Under certain natural restrictions, the conclusions of defeasible theories under the ambiguity propagating defeasible logic ADL correspond to those of the well-founded semantics for normal logic programs, and so it turns out that the two formalisms are closely related. Using the same translation of logic programs into defeasible theories, the semantics for the ambiguity blocking defeasible logic NDL can be seen as indirectly providing an ambiguity blocking semantics for logic programs. We also provide antimonotone operators for both ADL and NDL, each based on the Gelfond-Lifschitz (GL) operator for logic programs. For defeasible theories without defeaters or priorities on rules, the operator for ADL corresponds to the GL operator and so can be seen as partially capturing the consequences according to ADL. Similarly, the operator for NDL captures the consequences according to NDL, though in this case no restrictions on theories apply. Both operators can be used to define stable model semantics for defeasible theories.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge