FORBID: Fast Overlap Removal By stochastic gradIent Descent for Graph Drawing

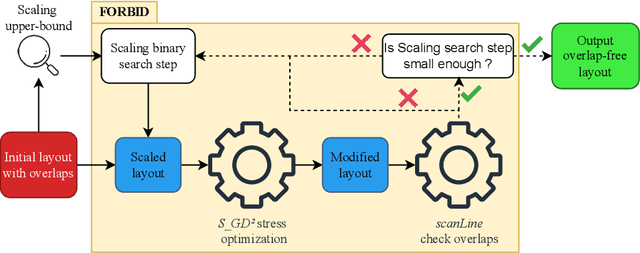
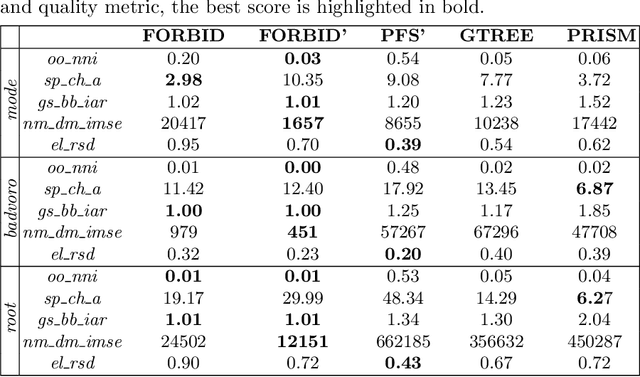
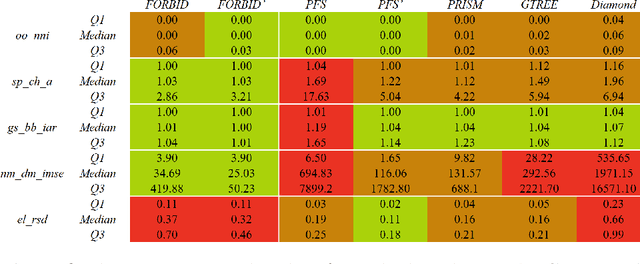
While many graph drawing algorithms consider nodes as points, graph visualization tools often represent them as shapes. These shapes support the display of information such as labels or encode various data with size or color. However, they can create overlaps between nodes which hinder the exploration process by hiding parts of the information. It is therefore of utmost importance to remove these overlaps to improve graph visualization readability. If not handled by the layout process, Overlap Removal (OR) algorithms have been proposed as layout post-processing. As graph layouts usually convey information about their topology, it is important that OR algorithms preserve them as much as possible. We propose a novel algorithm that models OR as a joint stress and scaling optimization problem, and leverages efficient stochastic gradient descent. This approach is compared with state-of-the-art algorithms, and several quality metrics demonstrate its efficiency to quickly remove overlaps while retaining the initial layout structures.

Deep Neural Network for DrawiNg Networks, ^2

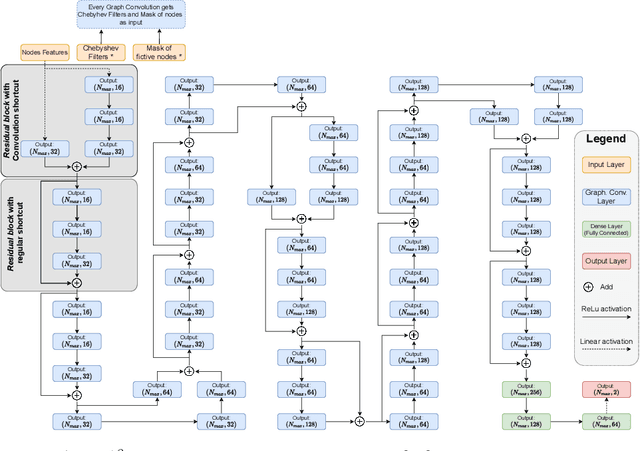
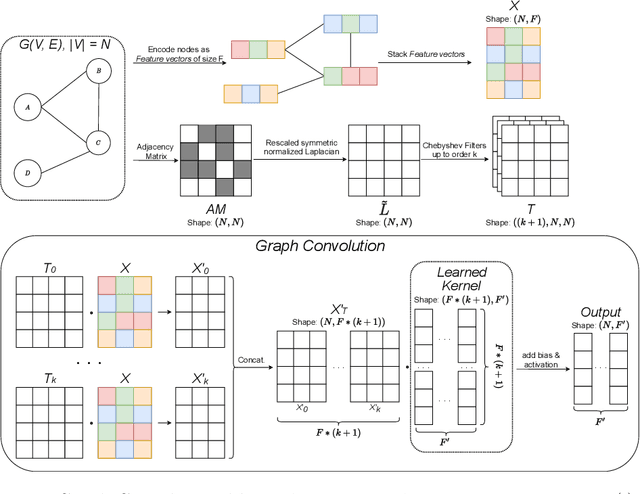
By leveraging recent progress of stochastic gradient descent methods, several works have shown that graphs could be efficiently laid out through the optimization of a tailored objective function. In the meantime, Deep Learning (DL) techniques achieved great performances in many applications. We demonstrate that it is possible to use DL techniques to learn a graph-to-layout sequence of operations thanks to a graph-related objective function. In this paper, we present a novel graph drawing framework called (DNN)^2: Deep Neural Network for DrawiNg Networks. Our method uses Graph Convolution Networks to learn a model. Learning is achieved by optimizing a graph topology related loss function that evaluates (DNN)^2 generated layouts during training. Once trained, the (DNN)^ model is able to quickly lay any input graph out. We experiment (DNN)^2 and statistically compare it to optimization-based and regular graph layout algorithms. The results show that (DNN)^2 performs well and are encouraging as the Deep Learning approach to Graph Drawing is novel and many leads for future works are identified.