FVV Live: A real-time free-viewpoint video system with consumer electronics hardware

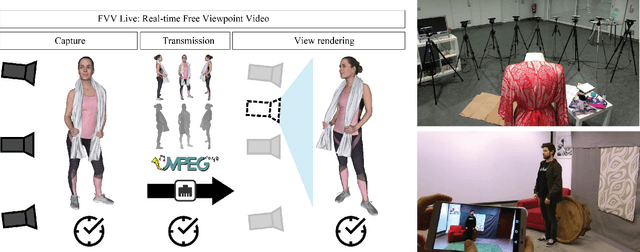
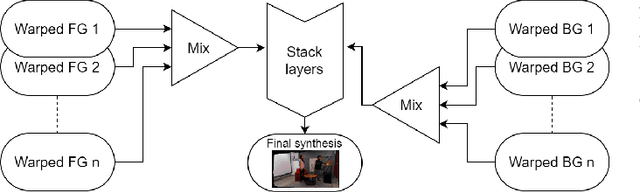
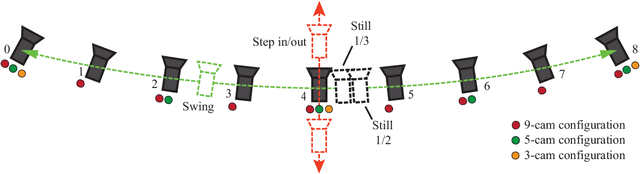
FVV Live is a novel end-to-end free-viewpoint video system, designed for low cost and real-time operation, based on off-the-shelf components. The system has been designed to yield high-quality free-viewpoint video using consumer-grade cameras and hardware, which enables low deployment costs and easy installation for immersive event-broadcasting or videoconferencing. The paper describes the architecture of the system, including acquisition and encoding of multiview plus depth data in several capture servers and virtual view synthesis on an edge server. All the blocks of the system have been designed to overcome the limitations imposed by hardware and network, which impact directly on the accuracy of depth data and thus on the quality of virtual view synthesis. The design of FVV Live allows for an arbitrary number of cameras and capture servers, and the results presented in this paper correspond to an implementation with nine stereo-based depth cameras. FVV Live presents low motion-to-photon and end-to-end delays, which enables seamless free-viewpoint navigation and bilateral immersive communications. Moreover, the visual quality of FVV Live has been assessed through subjective assessment with satisfactory results, and additional comparative tests show that it is preferred over state-of-the-art DIBR alternatives.

FVV Live: Real-Time, Low-Cost, Free Viewpoint Video

FVV Live is a novel real-time, low-latency, end-to-end free viewpoint system including capture, transmission, synthesis on an edge server and visualization and control on a mobile terminal. The system has been specially designed for low-cost and real-time operation, only using off-the-shelf components.

Optimal Piecewise Linear Function Approximation for GPU-based Applications

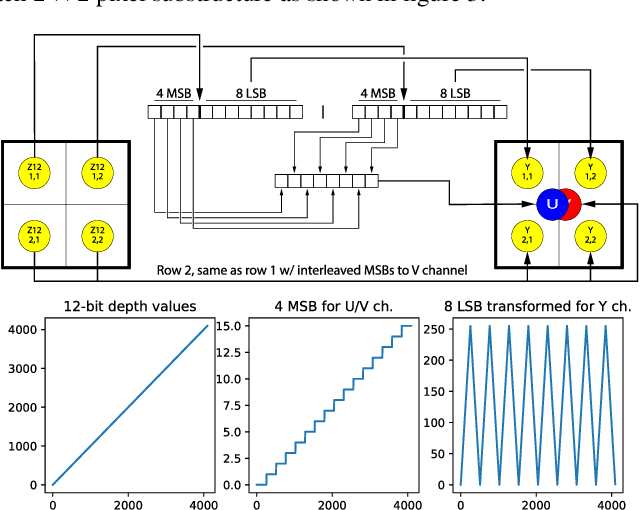
Many computer vision and human-computer interaction applications developed in recent years need evaluating complex and continuous mathematical functions as an essential step toward proper operation. However, rigorous evaluation of this kind of functions often implies a very high computational cost, unacceptable in real-time applications. To alleviate this problem, functions are commonly approximated by simpler piecewise-polynomial representations. Following this idea, we propose a novel, efficient, and practical technique to evaluate complex and continuous functions using a nearly optimal design of two types of piecewise linear approximations in the case of a large budget of evaluation subintervals. To this end, we develop a thorough error analysis that yields asymptotically tight bounds to accurately quantify the approximation performance of both representations. It provides an improvement upon previous error estimates and allows the user to control the trade-off between the approximation error and the number of evaluation subintervals. To guarantee real-time operation, the method is suitable for, but not limited to, an efficient implementation in modern Graphics Processing Units (GPUs), where it outperforms previous alternative approaches by exploiting the fixed-function interpolation routines present in their texture units. The proposed technique is a perfect match for any application requiring the evaluation of continuous functions, we have measured in detail its quality and efficiency on several functions, and, in particular, the Gaussian function because it is extensively used in many areas of computer vision and cybernetics, and it is expensive to evaluate.