Construction of the similarity matrix for the spectral clustering method: numerical experiments

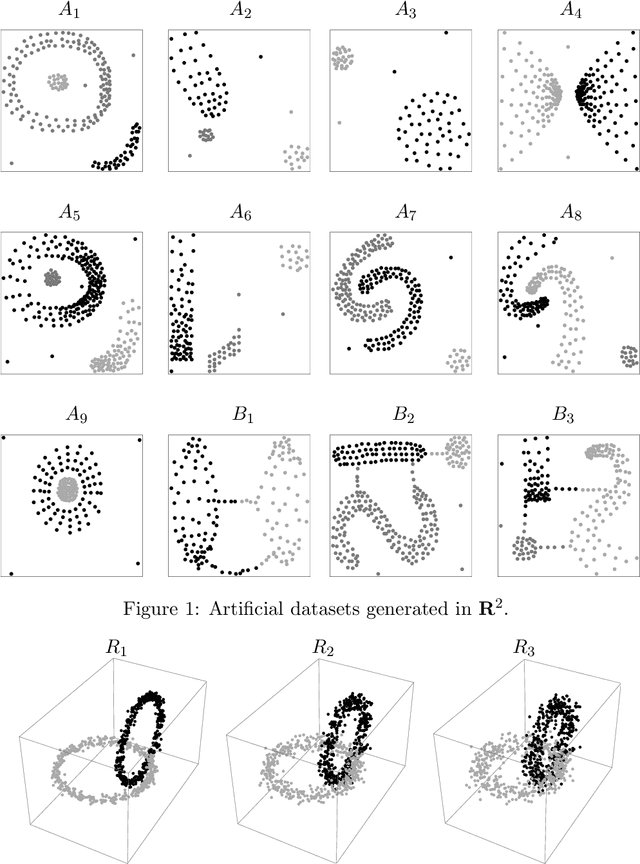
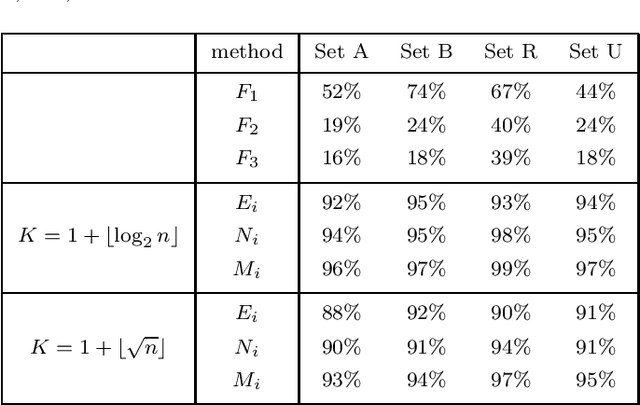
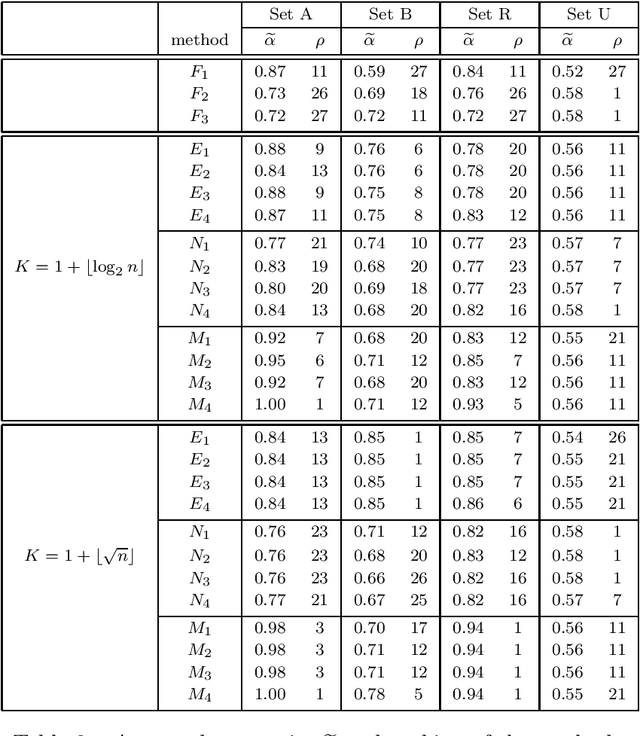
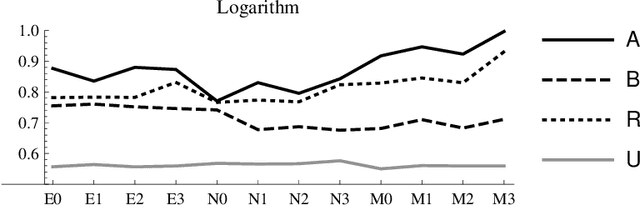
Spectral clustering is a powerful method for finding structure in a dataset through the eigenvectors of a similarity matrix. It often outperforms traditional clustering algorithms such as $k$-means when the structure of the individual clusters is highly non-convex. Its accuracy depends on how the similarity between pairs of data points is defined. Two important items contribute to the construction of the similarity matrix: the sparsity of the underlying weighted graph, which depends mainly on the distances among data points, and the similarity function. When a Gaussian similarity function is used, the choice of the scale parameter $\sigma$ can be critical. In this paper we examine both items, the sparsity and the selection of suitable $\sigma$'s, based either directly on the graph associated to the dataset or on the minimal spanning tree (MST) of the graph. An extensive numerical experimentation on artificial and real-world datasets has been carried out to compare the performances of the methods.

Adaptive Nonnegative Matrix Factorization and Measure Comparisons for Recommender Systems

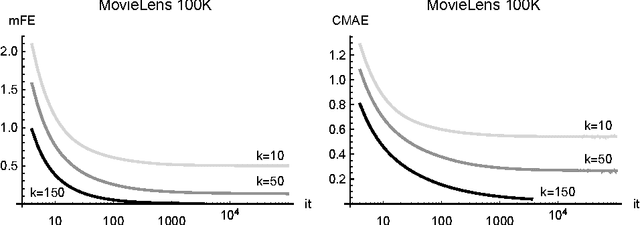
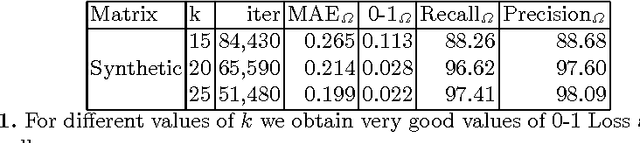
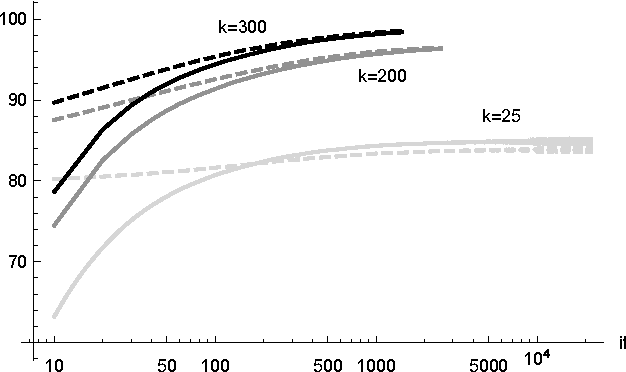
The Nonnegative Matrix Factorization (NMF) of the rating matrix has shown to be an effective method to tackle the recommendation problem. In this paper we propose new methods based on the NMF of the rating matrix and we compare them with some classical algorithms such as the SVD and the regularized and unregularized non-negative matrix factorization approach. In particular a new algorithm is obtained changing adaptively the function to be minimized at each step, realizing a sort of dynamic prior strategy. Another algorithm is obtained modifying the function to be minimized in the NMF formulation by enforcing the reconstruction of the unknown ratings toward a prior term. We then combine different methods obtaining two mixed strategies which turn out to be very effective in the reconstruction of missing observations. We perform a thoughtful comparison of different methods on the basis of several evaluation measures. We consider in particular rating, classification and ranking measures showing that the algorithm obtaining the best score for a given measure is in general the best also when different measures are considered, lowering the interest in designing specific evaluation measures. The algorithms have been tested on different datasets, in particular the 1M, and 10M MovieLens datasets containing ratings on movies, the Jester dataset with ranting on jokes and Amazon Fine Foods dataset with ratings on foods. The comparison of the different algorithms, shows the good performance of methods employing both an explicit and an implicit regularization scheme. Moreover we can get a boost by mixed strategies combining a fast method with a more accurate one.