Ornella Menchi
Construction of the similarity matrix for the spectral clustering method: numerical experiments
Apr 24, 2019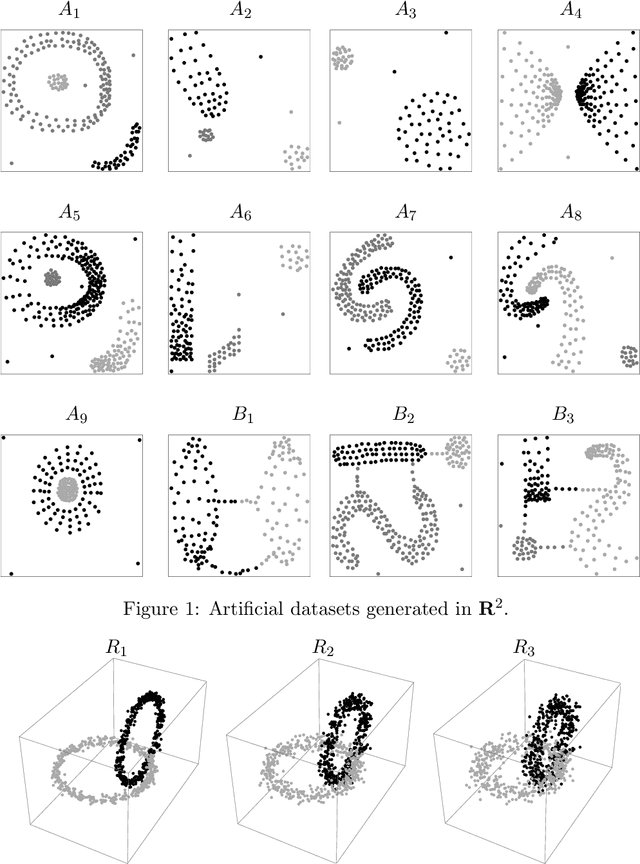
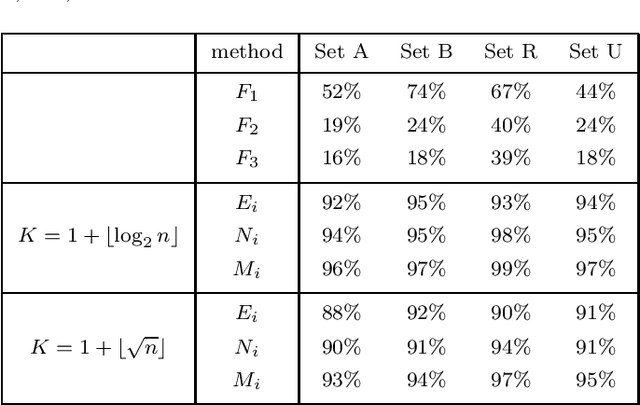
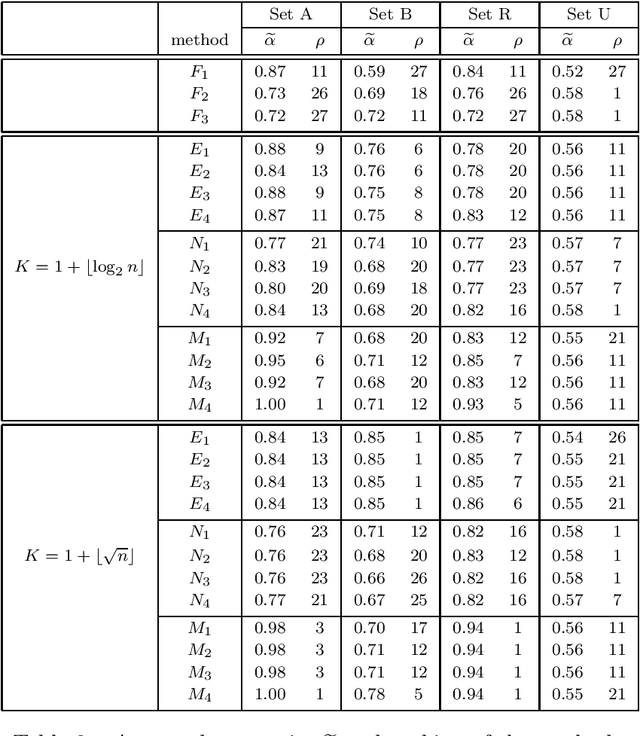
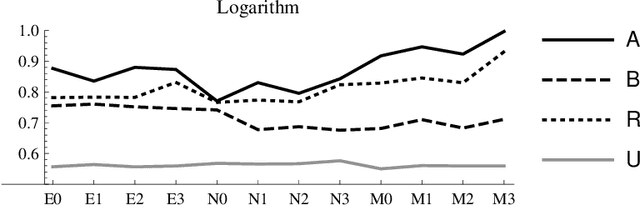
Abstract:Spectral clustering is a powerful method for finding structure in a dataset through the eigenvectors of a similarity matrix. It often outperforms traditional clustering algorithms such as $k$-means when the structure of the individual clusters is highly non-convex. Its accuracy depends on how the similarity between pairs of data points is defined. Two important items contribute to the construction of the similarity matrix: the sparsity of the underlying weighted graph, which depends mainly on the distances among data points, and the similarity function. When a Gaussian similarity function is used, the choice of the scale parameter $\sigma$ can be critical. In this paper we examine both items, the sparsity and the selection of suitable $\sigma$'s, based either directly on the graph associated to the dataset or on the minimal spanning tree (MST) of the graph. An extensive numerical experimentation on artificial and real-world datasets has been carried out to compare the performances of the methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge