Engineering morphogenesis of cell clusters with differentiable programming

Understanding the rules underlying organismal development is a major unsolved problem in biology. Each cell in a developing organism responds to signals in its local environment by dividing, excreting, consuming, or reorganizing, yet how these individual actions coordinate over a macroscopic number of cells to grow complex structures with exquisite functionality is unknown. Here we use recent advances in automatic differentiation to discover local interaction rules and genetic networks that yield emergent, systems-level characteristics in a model of development. We consider a growing tissue with cellular interactions are mediated by morphogen diffusion, differential cell adhesion and mechanical stress. Each cell has an internal genetic network that it uses to make decisions based on its local environment. We show that one can simultaneously learn parameters governing the cell interactions and the genetic network for complex developmental scenarios, including the symmetry breaking of an embryo from an initial cell, the creation of emergent chemical gradients,homogenization of growth via mechanical stress, programmed growth into a prespecified shape, and the ability to repair from damage. When combined with recent experimental advances measuring spatio-temporal dynamics and gene expression of cells in a growing tissue, the methodology outlined here offers a promising path to unravelling the cellular basis of development.

Simplex2Vec embeddings for community detection in simplicial complexes

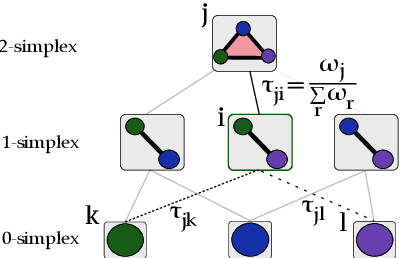
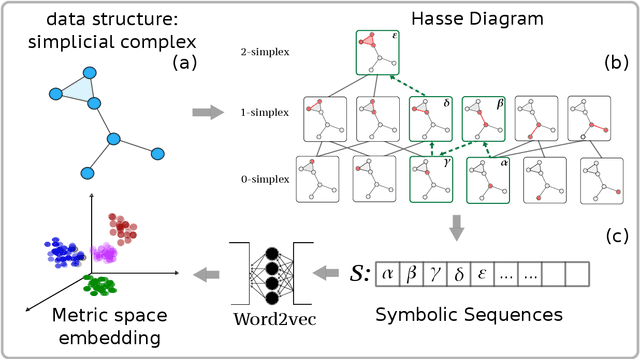
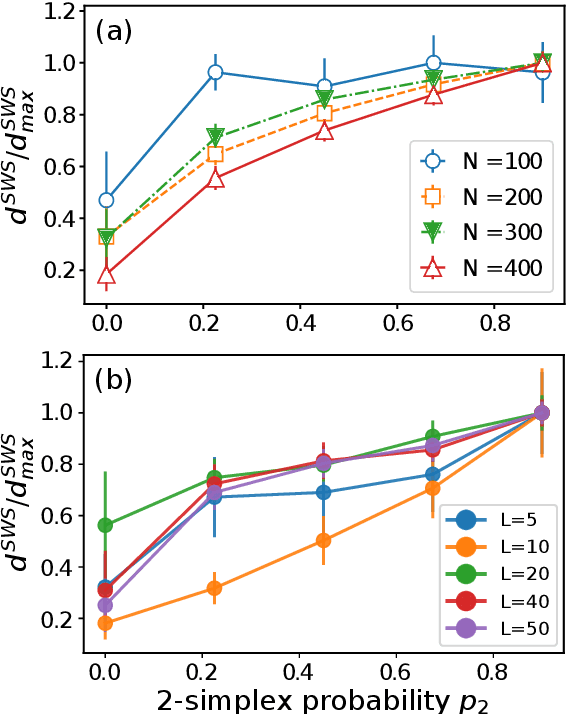
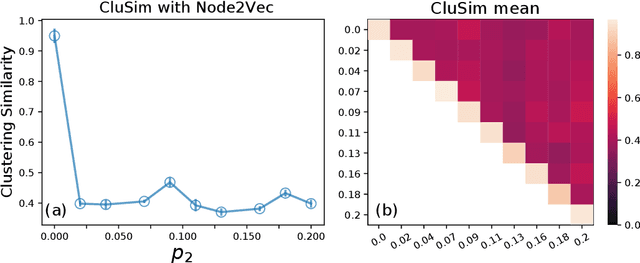
Topological representations are rapidly becoming a popular way to capture and encode higher-order interactions in complex systems. They have found applications in disciplines as different as cancer genomics, brain function, and computational social science, in representing both descriptive features of data and inference models. While intense research has focused on the connectivity and homological features of topological representations, surprisingly scarce attention has been given to the investigation of the community structures of simplicial complexes. To this end, we adopt recent advances in symbolic embeddings to compute and visualize the community structures of simplicial complexes. We first investigate the stability properties of embedding obtained for synthetic simplicial complexes to the presence of higher order interactions. We then focus on complexes arising from social and brain functional data and show how higher order interactions can be leveraged to improve clustering detection and assess the effect of higher order interaction on individual nodes. We conclude delineating limitations and directions for extension of this work.