Francesco Landolfi
Constraint-Free Structure Learning with Smooth Acyclic Orientations
Sep 15, 2023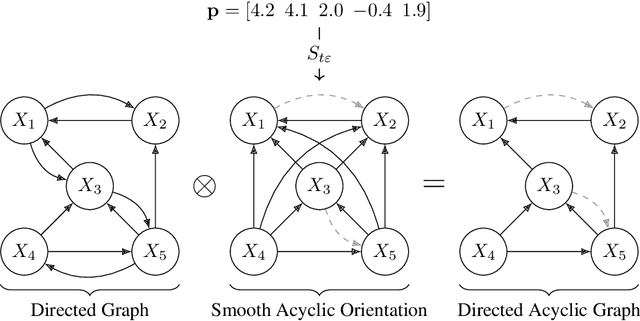
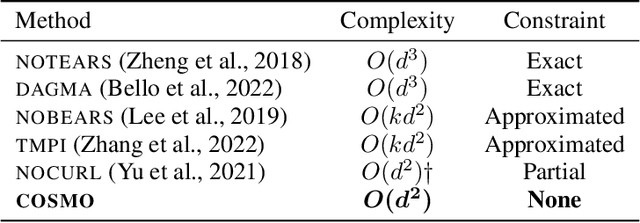
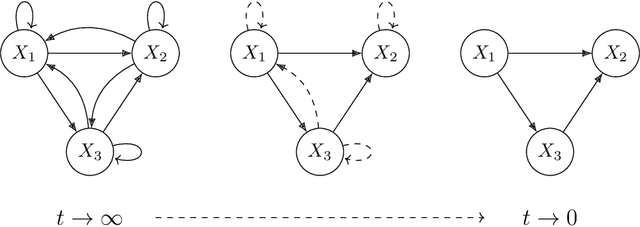
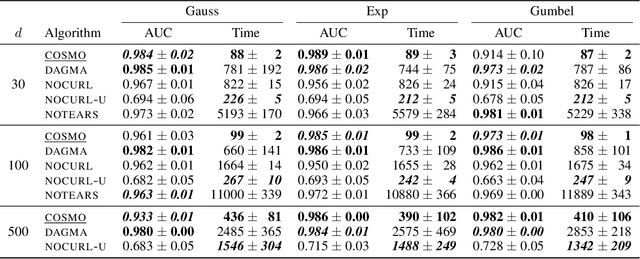
Abstract:The structure learning problem consists of fitting data generated by a Directed Acyclic Graph (DAG) to correctly reconstruct its arcs. In this context, differentiable approaches constrain or regularize the optimization problem using a continuous relaxation of the acyclicity property. The computational cost of evaluating graph acyclicity is cubic on the number of nodes and significantly affects scalability. In this paper we introduce COSMO, a constraint-free continuous optimization scheme for acyclic structure learning. At the core of our method, we define a differentiable approximation of an orientation matrix parameterized by a single priority vector. Differently from previous work, our parameterization fits a smooth orientation matrix and the resulting acyclic adjacency matrix without evaluating acyclicity at any step. Despite the absence of explicit constraints, we prove that COSMO always converges to an acyclic solution. In addition to being asymptotically faster, our empirical analysis highlights how COSMO performance on graph reconstruction compares favorably with competing structure learning methods.
Graph Pooling with Maximum-Weight $k$-Independent Sets
Aug 06, 2022Abstract:Graph reductions are fundamental when dealing with large scale networks and relational data. They allow to downsize tasks of high computational impact by solving them in coarsened structures. At the same time, graph reductions play the role of pooling layers in graph neural networks, to extract multi-resolution representations from structures. In these contexts, the ability of the reduction mechanism to preserve distance relationships and topological properties appears fundamental, along with a scalability enabling its application to real-world sized problems. In this paper, we introduce a graph coarsening mechanism based on the graph-theoretic concept of maximum-weight $k$-independent sets, providing a greedy algorithm that allows efficient parallel implementation on GPUs. Our method is the first graph-structured counterpart of controllable equispaced coarsening mechanisms in regular data (images, sequences). We prove theoretical guarantees for distortion bounds on path lengths, as well as the ability to preserve key topological properties in the coarsened graphs. We leverage these concepts to define a graph pooling mechanism that we empirically assess in graph classification tasks, showing that it compares favorably against pooling methods in literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge