François-Pierre Paty
Algorithms for Weak Optimal Transport with an Application to Economics
May 23, 2022
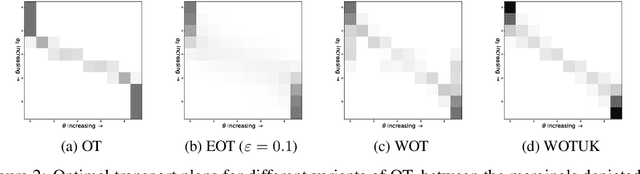
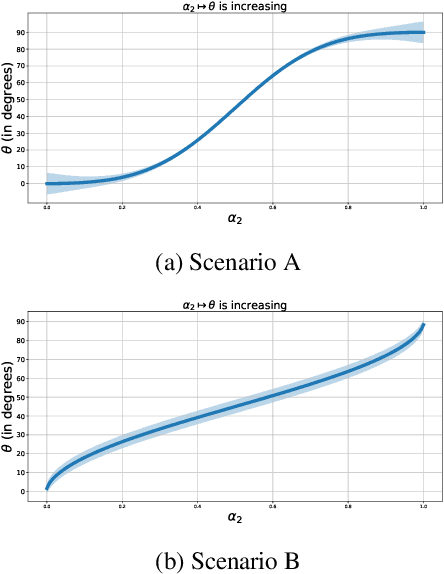
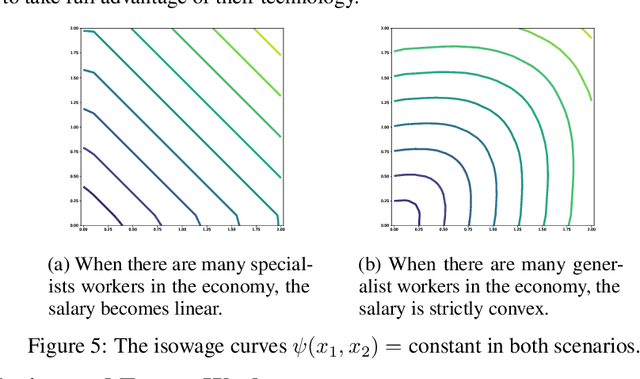
Abstract:The theory of weak optimal transport (WOT), introduced by [Gozlan et al., 2017], generalizes the classic Monge-Kantorovich framework by allowing the transport cost between one point and the points it is matched with to be nonlinear. In the so-called barycentric version of WOT, the cost for transporting a point $x$ only depends on $x$ and on the barycenter of the points it is matched with. This aggregation property of WOT is appealing in machine learning, economics and finance. Yet algorithms to compute WOT have only been developed for the special case of quadratic barycentric WOT, or depend on neural networks with no guarantee on the computed value and matching. The main difficulty lies in the transportation constraints which are costly to project onto. In this paper, we propose to use mirror descent algorithms to solve the primal and dual versions of the WOT problem. We also apply our algorithms to the variant of WOT introduced by [Chon\'e et al., 2022] where mass is distributed from one space to another through unnormalized kernels (WOTUK). We empirically compare the solutions of WOT and WOTUK with classical OT. We illustrate our numerical methods to the economic framework of [Chon\'e and Kramarz, 2021], namely the matching between workers and firms on labor markets.
Regularized Optimal Transport is Ground Cost Adversarial
Feb 10, 2020



Abstract:Regularizing Wasserstein distances has proved to be the key in the recent advances of optimal transport (OT) in machine learning. Most prominent is the entropic regularization of OT, which not only allows for fast computations and differentiation using Sinkhorn algorithm, but also improves stability with respect to data and accuracy in many numerical experiments. Theoretical understanding of these benefits remains unclear, although recent statistical works have shown that entropy-regularized OT mitigates classical OT's curse of dimensionality. In this paper, we adopt a more geometrical point of view, and show using Fenchel duality that any convex regularization of OT can be interpreted as ground cost adversarial. This incidentally gives access to a robust dissimilarity measure on the ground space, which can in turn be used in other applications. We propose algorithms to compute this robust cost, and illustrate the interest of this approach empirically.
Regularity as Regularization: Smooth and Strongly Convex Brenier Potentials in Optimal Transport
Jun 03, 2019



Abstract:The problem of estimating Wasserstein distances in high-dimensional spaces suffers from the curse of dimensionality: One needs an exponential (w.r.t. dimension) number of samples for the distance between two measures to be comparable to that evaluated using i.i.d samples. Therefore, using the optimal transport (OT) geometry in machine learning involves regularizing it, one way or another. One of the greatest achievements of the OT literature in recent years lies in regularity theory: one can prove under suitable hypothesis that the OT map between two measures is Lipschitz, or, equivalently when studying 2-Wasserstein distances, that the Brenier convex potential (whose gradient yields an optimal map) is a smooth function. We propose in this work to go backwards, and adopt instead regularity as a regularization tool. We propose algorithms working on discrete measures that can recover nearly optimal transport maps that have small distortion, or, equivalently, nearly optimal Brenier potential that are strongly convex and smooth. For univariate measures, we show that computing these potentials is equivalent to solving an isotonic regression problem under Lipschitz and strong monotonicity constraints. For multivariate measures the problem boils down to a non-convex QCQP problem, which can be relaxed to a semidefinite program. Most importantly, we recover as the result of this optimization the values and gradients of the Brenier potential on sampled points, but show how that they can be more generally evaluated on any new point, at the cost of solving a QP for each new evaluation. Building on these two formulations we propose practical algorithms to estimate and evaluate transport maps with desired smoothness/strong convexity properties, illustrate their statistical performance and visualize maps on a color transfer task.
Subspace Robust Wasserstein Distances
Feb 04, 2019



Abstract:Making sense of Wasserstein distances between discrete measures in high-dimensional settings remains a challenge. Recent work has advocated a two-step approach to improve robustness and facilitate the computation of optimal transport, using for instance projections on random real lines, or a preliminary quantization of the measures to reduce the size of their support. We propose in this work a max-min robust variant of the Wasserstein distance by considering the maximal possible distance that can be realized between two measures, assuming they can be projected orthogonally on a lower $k$-dimensional subspace. Alternatively, we show that the corresponding min-max OT problem has a tight convex relaxation which can be cast as that of finding an optimal transport plan with a low transportation cost, where that the cost is alternatively defined as the sum of the $k$ largest eigenvalues of the second order moment matrix of the displacements (or matchings) corresponding to that plan (the usual OT definition only considers the trace of that matrix). We show that both quantities inherit several favorably properties from the OT geometry. We propose two algorithms to compute the latter formulation using entropic regularization, and illustrate the interest of this approach empirically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge