Francis Kramarz
Graphon Estimation in bipartite graphs with observable edge labels and unobservable node labels
Apr 07, 2023Abstract:Many real-world data sets can be presented in the form of a matrix whose entries correspond to the interaction between two entities of different natures (number of times a web user visits a web page, a student's grade in a subject, a patient's rating of a doctor, etc.). We assume in this paper that the mentioned interaction is determined by unobservable latent variables describing each entity. Our objective is to estimate the conditional expectation of the data matrix given the unobservable variables. This is presented as a problem of estimation of a bivariate function referred to as graphon. We study the cases of piecewise constant and H\"older-continuous graphons. We establish finite sample risk bounds for the least squares estimator and the exponentially weighted aggregate. These bounds highlight the dependence of the estimation error on the size of the data set, the maximum intensity of the interactions, and the level of noise. As the analyzed least-squares estimator is intractable, we propose an adaptation of Lloyd's alternating minimization algorithm to compute an approximation of the least-squares estimator. Finally, we present numerical experiments in order to illustrate the empirical performance of the graphon estimator on synthetic data sets.
Algorithms for Weak Optimal Transport with an Application to Economics
May 23, 2022
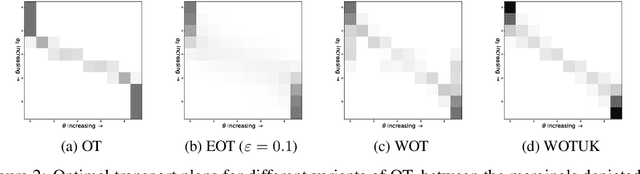
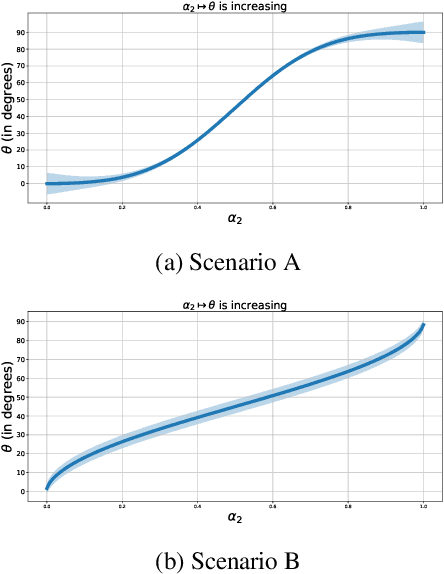
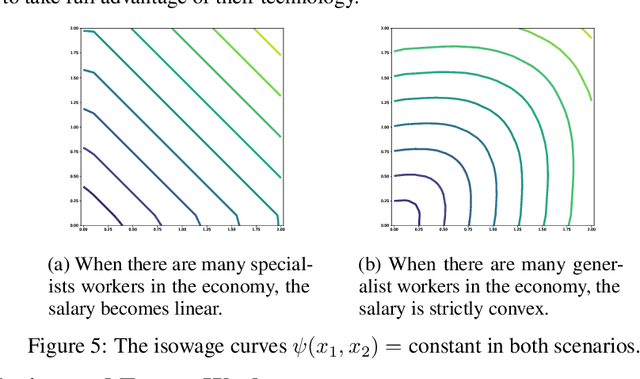
Abstract:The theory of weak optimal transport (WOT), introduced by [Gozlan et al., 2017], generalizes the classic Monge-Kantorovich framework by allowing the transport cost between one point and the points it is matched with to be nonlinear. In the so-called barycentric version of WOT, the cost for transporting a point $x$ only depends on $x$ and on the barycenter of the points it is matched with. This aggregation property of WOT is appealing in machine learning, economics and finance. Yet algorithms to compute WOT have only been developed for the special case of quadratic barycentric WOT, or depend on neural networks with no guarantee on the computed value and matching. The main difficulty lies in the transportation constraints which are costly to project onto. In this paper, we propose to use mirror descent algorithms to solve the primal and dual versions of the WOT problem. We also apply our algorithms to the variant of WOT introduced by [Chon\'e et al., 2022] where mass is distributed from one space to another through unnormalized kernels (WOTUK). We empirically compare the solutions of WOT and WOTUK with classical OT. We illustrate our numerical methods to the economic framework of [Chon\'e and Kramarz, 2021], namely the matching between workers and firms on labor markets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge