In almost all shallow analytic neural network optimization landscapes, efficient minimizers have strongly convex neighborhoods

Whether or not a local minimum of a cost function has a strongly convex neighborhood greatly influences the asymptotic convergence rate of optimizers. In this article, we rigorously analyze the prevalence of this property for the mean squared error induced by shallow, 1-hidden layer neural networks with analytic activation functions when applied to regression problems. The parameter space is divided into two domains: the 'efficient domain' (all parameters for which the respective realization function cannot be generated by a network having a smaller number of neurons) and the 'redundant domain' (the remaining parameters). In almost all regression problems on the efficient domain the optimization landscape only features local minima that are strongly convex. Formally, we will show that for certain randomly picked regression problems the optimization landscape is almost surely a Morse function on the efficient domain. The redundant domain has significantly smaller dimension than the efficient domain and on this domain, potential local minima are never isolated.

Gradient Span Algorithms Make Predictable Progress in High Dimension

We prove that all 'gradient span algorithms' have asymptotically deterministic behavior on scaled Gaussian random functions as the dimension tends to infinity. In particular, this result explains the counterintuitive phenomenon that different training runs of many large machine learning models result in approximately equal cost curves despite random initialization on a complicated non-convex landscape. The distributional assumption of (non-stationary) isotropic Gaussian random functions we use is sufficiently general to serve as realistic model for machine learning training but also encompass spin glasses and random quadratic functions.

Random Function Descent

While gradient based methods are ubiquitous in machine learning, selecting the right step size often requires "hyperparameter tuning". This is because backtracking procedures like Armijo's rule depend on quality evaluations in every step, which are not available in a stochastic context. Since optimization schemes can be motivated using Taylor approximations, we replace the Taylor approximation with the conditional expectation (the best $L^2$ estimator) and propose "Random Function Descent" (RFD). Under light assumptions common in Bayesian optimization, we prove that RFD is identical to gradient descent, but with calculable step sizes, even in a stochastic context. We beat untuned Adam in synthetic benchmarks. To close the performance gap to tuned Adam, we propose a heuristic extension competitive with tuned Adam.

High Dimensional Optimization through the Lens of Machine Learning

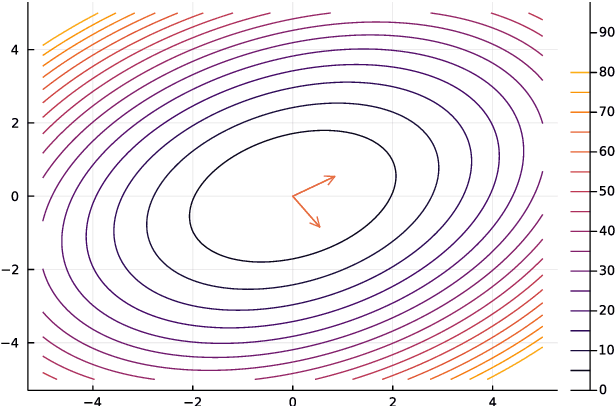
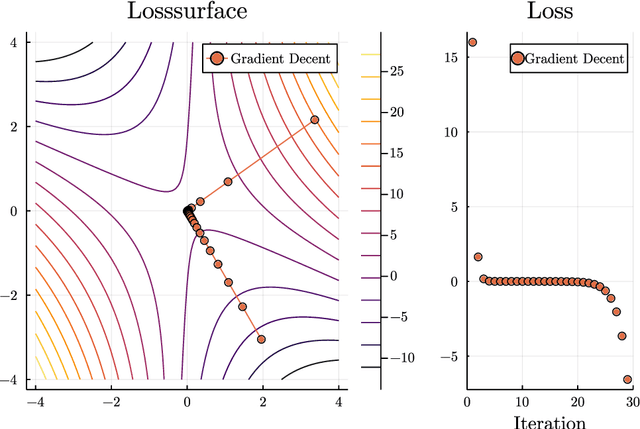
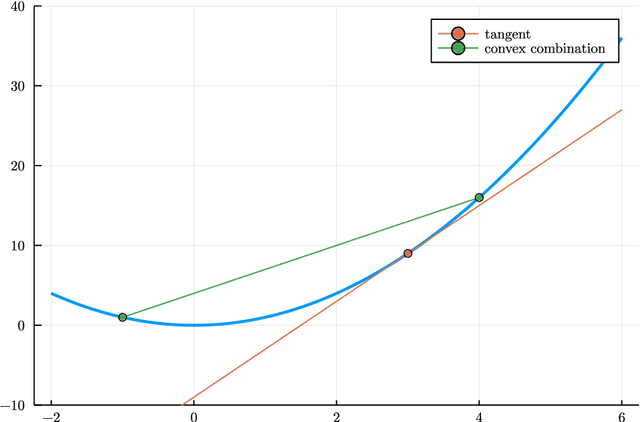
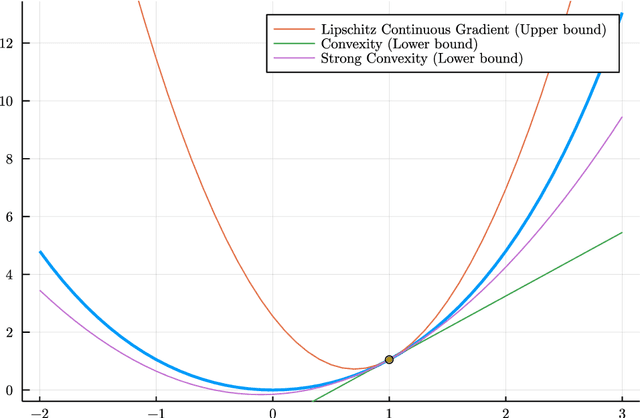
This thesis reviews numerical optimization methods with machine learning problems in mind. Since machine learning models are highly parametrized, we focus on methods suited for high dimensional optimization. We build intuition on quadratic models to figure out which methods are suited for non-convex optimization, and develop convergence proofs on convex functions for this selection of methods. With this theoretical foundation for stochastic gradient descent and momentum methods, we try to explain why the methods used commonly in the machine learning field are so successful. Besides explaining successful heuristics, the last chapter also provides a less extensive review of more theoretical methods, which are not quite as popular in practice. So in some sense this work attempts to answer the question: Why are the default Tensorflow optimizers included in the defaults?