High Dimensional Optimization through the Lens of Machine Learning
Paper and Code
Dec 31, 2021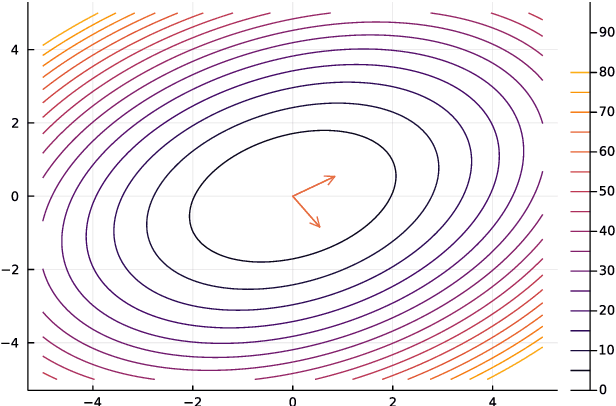
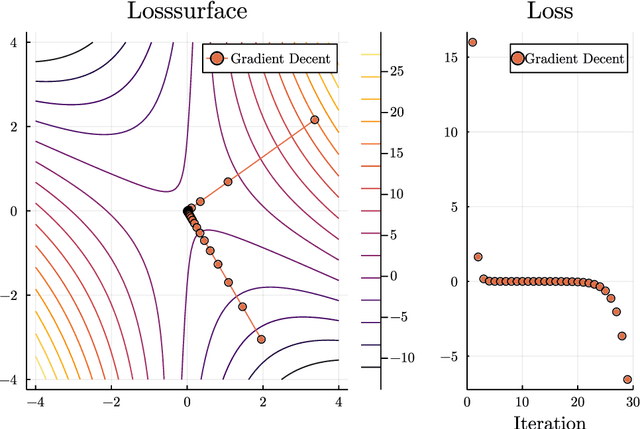
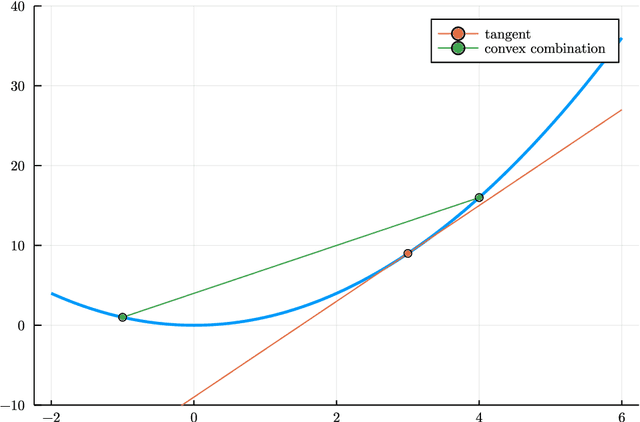
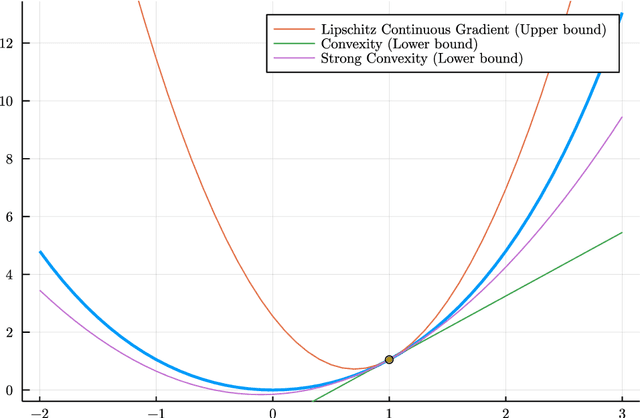
This thesis reviews numerical optimization methods with machine learning problems in mind. Since machine learning models are highly parametrized, we focus on methods suited for high dimensional optimization. We build intuition on quadratic models to figure out which methods are suited for non-convex optimization, and develop convergence proofs on convex functions for this selection of methods. With this theoretical foundation for stochastic gradient descent and momentum methods, we try to explain why the methods used commonly in the machine learning field are so successful. Besides explaining successful heuristics, the last chapter also provides a less extensive review of more theoretical methods, which are not quite as popular in practice. So in some sense this work attempts to answer the question: Why are the default Tensorflow optimizers included in the defaults?
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge