A Self-supervised Approach to Hierarchical Forecasting with Applications to Groupwise Synthetic Controls

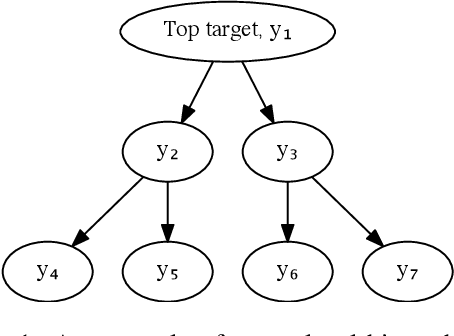
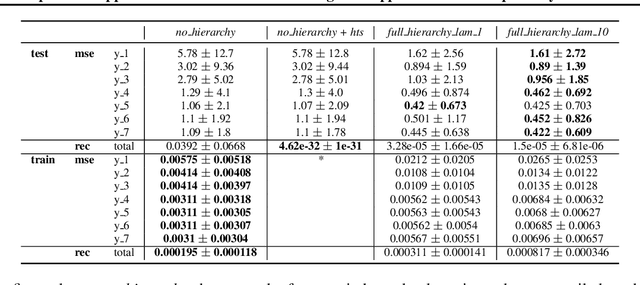
When forecasting time series with a hierarchical structure, the existing state of the art is to forecast each time series independently, and, in a post-treatment step, to reconcile the time series in a way that respects the hierarchy (Hyndman et al., 2011; Wickramasuriya et al., 2018). We propose a new loss function that can be incorporated into any maximum likelihood objective with hierarchical data, resulting in reconciled estimates with confidence intervals that correctly account for additional uncertainty due to imperfect reconciliation. We evaluate our method using a non-linear model and synthetic data on a counterfactual forecasting problem, where we have access to the ground truth and contemporaneous covariates, and show that we largely improve over the existing state-of-the-art method.

GANs for Biological Image Synthesis

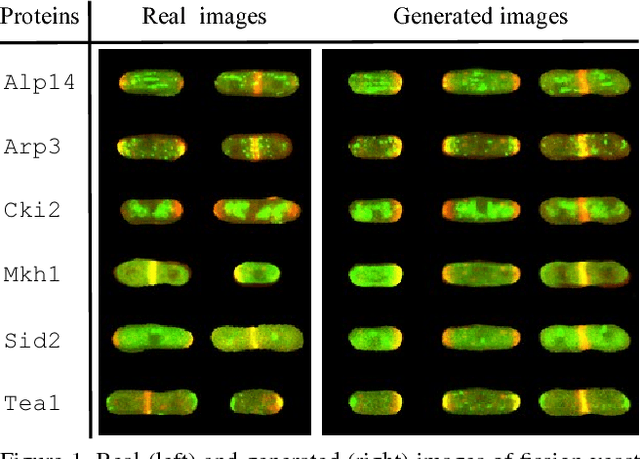
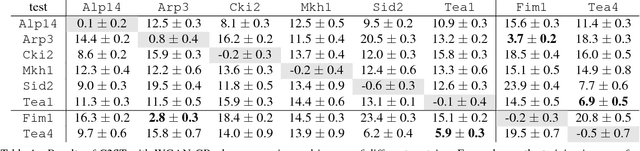
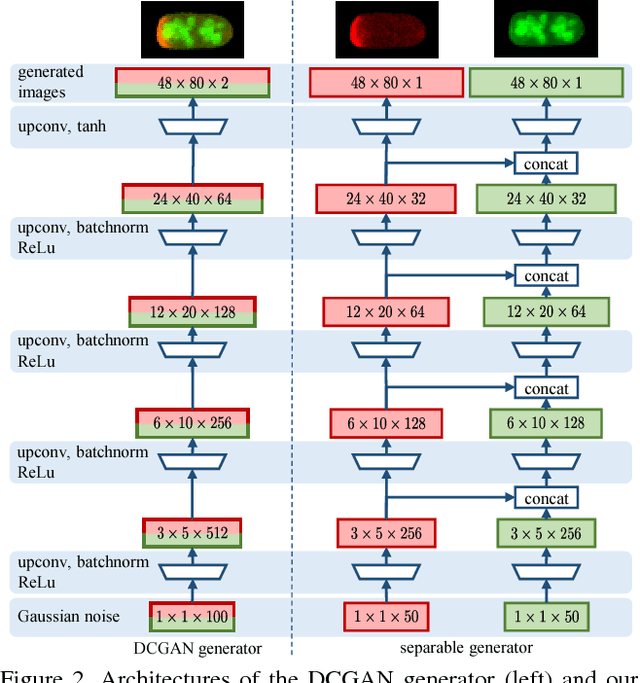
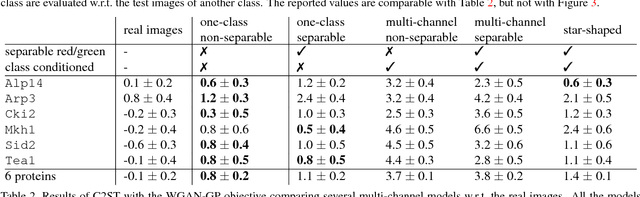
In this paper, we propose a novel application of Generative Adversarial Networks (GAN) to the synthesis of cells imaged by fluorescence microscopy. Compared to natural images, cells tend to have a simpler and more geometric global structure that facilitates image generation. However, the correlation between the spatial pattern of different fluorescent proteins reflects important biological functions, and synthesized images have to capture these relationships to be relevant for biological applications. We adapt GANs to the task at hand and propose new models with casual dependencies between image channels that can generate multi-channel images, which would be impossible to obtain experimentally. We evaluate our approach using two independent techniques and compare it against sensible baselines. Finally, we demonstrate that by interpolating across the latent space we can mimic the known changes in protein localization that occur through time during the cell cycle, allowing us to predict temporal evolution from static images.