Spatio-temporal estimation of wind speed and wind power using machine learning: predictions, uncertainty and technical potential

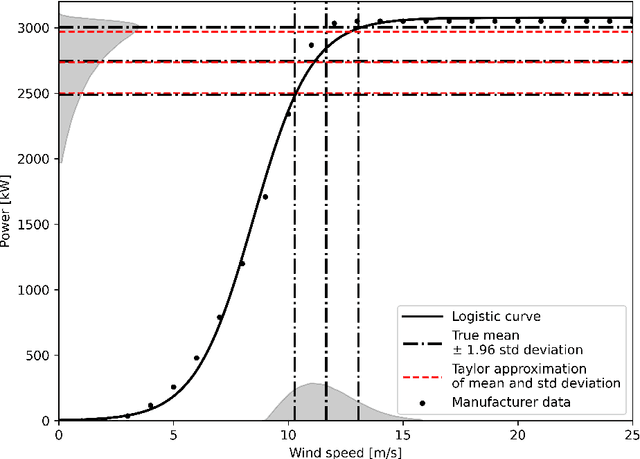
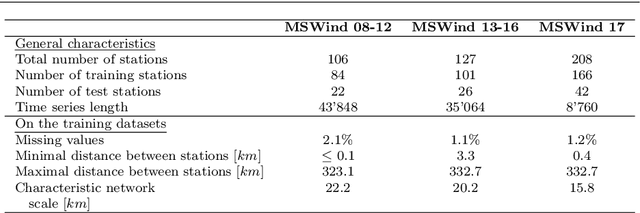
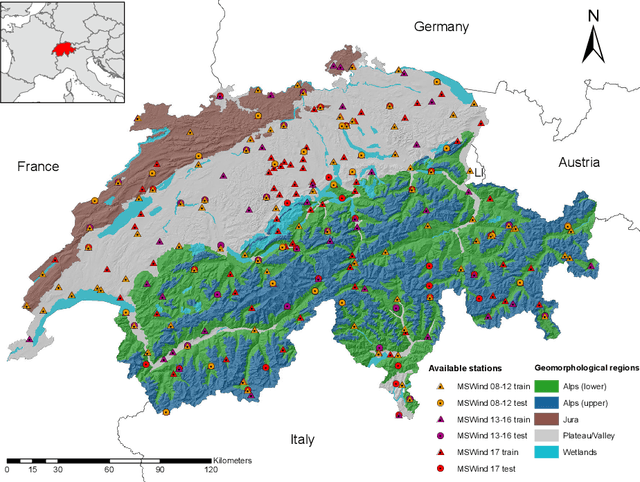
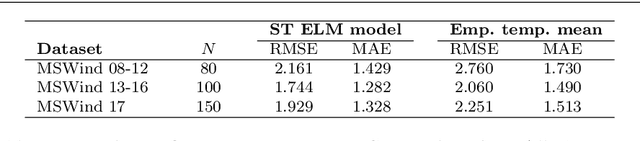
The growth of wind generation capacities in the past decades has shown that wind energy can contribute to the energy transition in many parts of the world. Being highly variable and complex to model, the quantification of the spatio-temporal variation of wind power and the related uncertainty is highly relevant for energy planners. Machine Learning has become a popular tool to perform wind-speed and power predictions. However, the existing approaches have several limitations. These include (i) insufficient consideration of spatio-temporal correlations in wind-speed data, (ii) a lack of existing methodologies to quantify the uncertainty of wind speed prediction and its propagation to the wind-power estimation, and (iii) a focus on less than hourly frequencies. To overcome these limitations, we introduce a framework to reconstruct a spatio-temporal field on a regular grid from irregularly distributed wind-speed measurements. After decomposing data into temporally referenced basis functions and their corresponding spatially distributed coefficients, the latter are spatially modelled using Extreme Learning Machines. Estimates of both model and prediction uncertainties, and of their propagation after the transformation of wind speed into wind power, are then provided without any assumptions on distribution patterns of the data. The methodology is applied to the study of hourly wind power potential on a grid of $250\times 250$ m$^2$ for turbines of 100 meters hub height in Switzerland, generating the first dataset of its type for the country. The potential wind power generation is combined with the available area for wind turbine installations to yield an estimate of the technical potential for wind power in Switzerland. The wind power estimate presented here represents an important input for planners to support the design of future energy systems with increased wind power generation.

Uncertainty Quantification in Extreme Learning Machine: Analytical Developments, Variance Estimates and Confidence Intervals

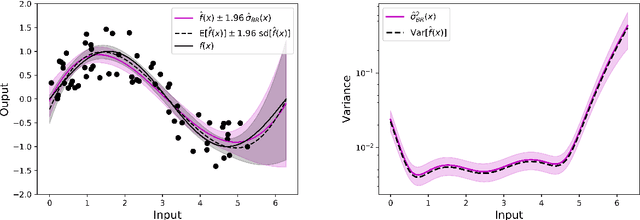
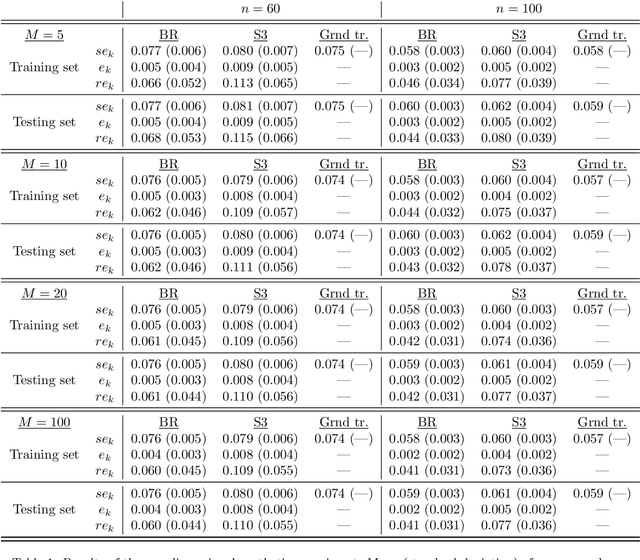
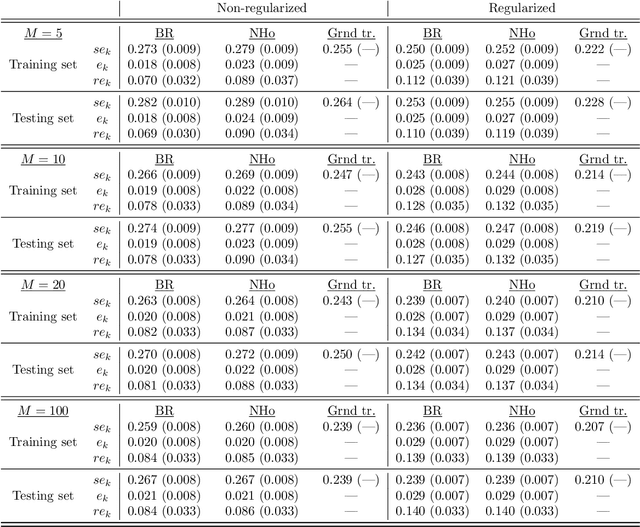
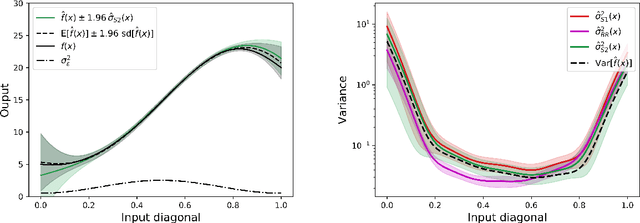
Uncertainty quantification is crucial to assess prediction quality of a machine learning model. In the case of Extreme Learning Machines (ELM), most methods proposed in the literature make strong assumptions on the data, ignore the randomness of input weights or neglect the bias contribution in confidence interval estimations. This paper presents novel estimations that overcome these constraints and improve the understanding of ELM variability. Analytical derivations are provided under general assumptions, supporting the identification and the interpretation of the contribution of different variability sources. Under both homoskedasticity and heteroskedasticity, several variance estimates are proposed, investigated, and numerically tested, showing their effectiveness in replicating the expected variance behaviours. Finally, the feasibility of confidence intervals estimation is discussed by adopting a critical approach, hence raising the awareness of ELM users concerning some of their pitfalls. The paper is accompanied with a scikit-learn compatible Python library enabling efficient computation of all estimates discussed herein.

On Feature Selection Using Anisotropic General Regression Neural Network

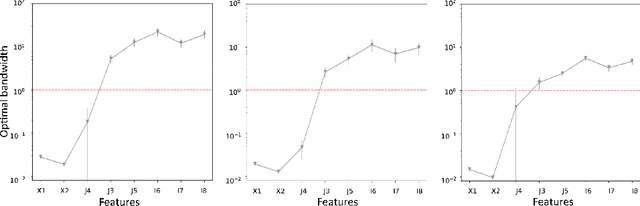
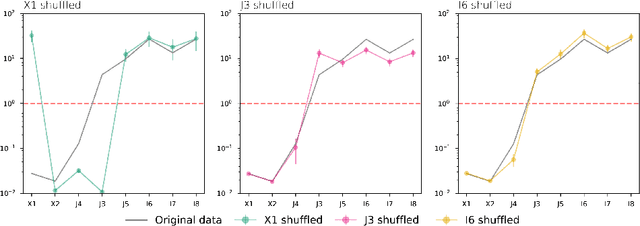
The presence of irrelevant features in the input dataset tends to reduce the interpretability and predictive quality of machine learning models. Therefore, the development of feature selection methods to recognize irrelevant features is a crucial topic in machine learning. Here we show how the General Regression Neural Network used with an anisotropic Gaussian Kernel can be used to perform feature selection. A number of numerical experiments are conducted using simulated data to study the robustness of the proposed methodology and its sensitivity to sample size. Finally, a comparison with four other feature selection methods is performed on several real world datasets.

A Novel Framework for Spatio-Temporal Prediction of Climate Data Using Deep Learning

As the role played by statistical and computational sciences in climate modelling and prediction becomes more important, Machine Learning researchers are becoming more aware of the relevance of their work to help tackle the climate crisis. Indeed, being universal nonlinear fucntion approximation tools, Machine Learning algorithms are efficient in analysing and modelling spatially and temporally variable climate data. While Deep Learning models have proved to be able to capture spatial, temporal, and spatio-temporal dependencies through their automatic feature representation learning, the problem of the interpolation of continuous spatio-temporal fields measured on a set of irregular points in space is still under-investigated. To fill this gap, we introduce here a framework for spatio-temporal prediction of climate and environmental data using deep learning. Specifically, we show how spatio-temporal processes can be decomposed in terms of a sum of products of temporally referenced basis functions, and of stochastic spatial coefficients which can be spatially modelled and mapped on a regular grid, allowing the reconstruction of the complete spatio-temporal signal. Applications on two case studies based on simulated and real-world data will show the effectiveness of the proposed framework in modelling coherent spatio-temporal fields.