Fabrizio Rggeri
Optimal partitioning of directed acyclic graphs with dependent costs between clusters
Aug 08, 2023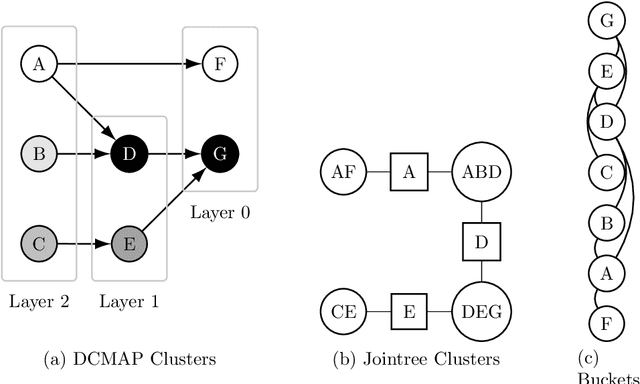
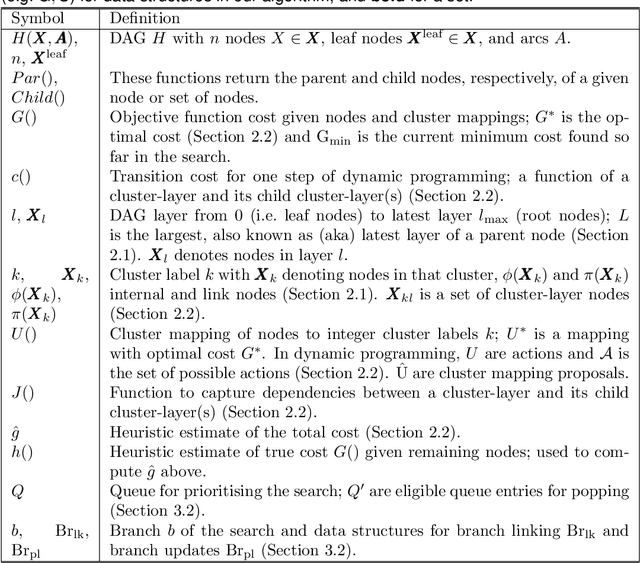

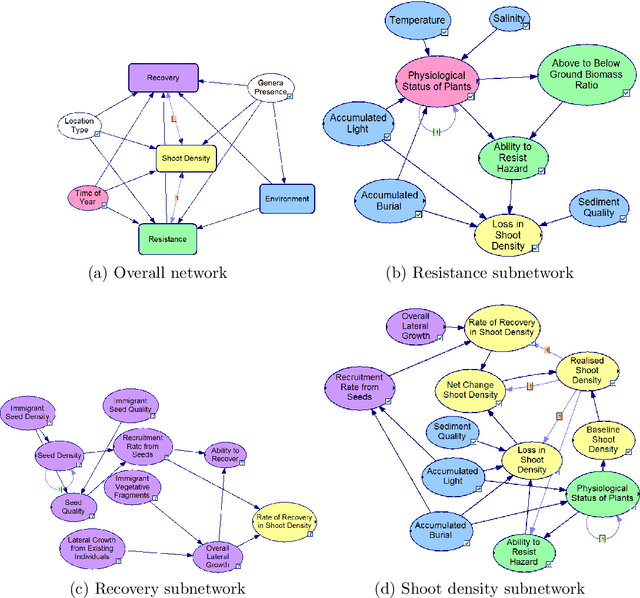
Abstract:Many statistical inference contexts, including Bayesian Networks (BNs), Markov processes and Hidden Markov Models (HMMS) could be supported by partitioning (i.e.~mapping) the underlying Directed Acyclic Graph (DAG) into clusters. However, optimal partitioning is challenging, especially in statistical inference as the cost to be optimised is dependent on both nodes within a cluster, and the mapping of clusters connected via parent and/or child nodes, which we call dependent clusters. We propose a novel algorithm called DCMAP for optimal cluster mapping with dependent clusters. Given an arbitrarily defined, positive cost function based on the DAG and cluster mappings, we show that DCMAP converges to find all optimal clusters, and returns near-optimal solutions along the way. Empirically, we find that the algorithm is time-efficient for a DBN model of a seagrass complex system using a computation cost function. For a 25 and 50-node DBN, the search space size was $9.91\times 10^9$ and $1.51\times10^{21}$ possible cluster mappings, respectively, but near-optimal solutions with 88\% and 72\% similarity to the optimal solution were found at iterations 170 and 865, respectively. The first optimal solution was found at iteration 934 $(\text{95\% CI } 926,971)$, and 2256 $(2150,2271)$ with a cost that was 4\% and 0.2\% of the naive heuristic cost, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge