Fabrizio Angaroni
EAD: an ensemble approach to detect adversarial examples from the hidden features of deep neural networks
Nov 25, 2021
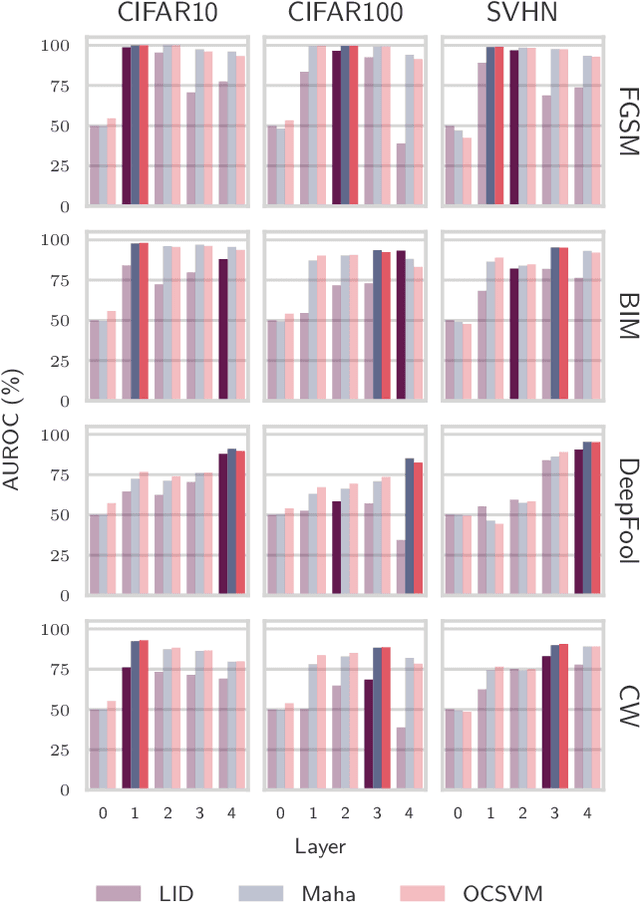


Abstract:One of the key challenges in Deep Learning is the definition of effective strategies for the detection of adversarial examples. To this end, we propose a novel approach named Ensemble Adversarial Detector (EAD) for the identification of adversarial examples, in a standard multiclass classification scenario. EAD combines multiple detectors that exploit distinct properties of the input instances in the internal representation of a pre-trained Deep Neural Network (DNN). Specifically, EAD integrates the state-of-the-art detectors based on Mahalanobis distance and on Local Intrinsic Dimensionality (LID) with a newly introduced method based on One-class Support Vector Machines (OSVMs). Although all constituting methods assume that the greater the distance of a test instance from the set of correctly classified training instances, the higher its probability to be an adversarial example, they differ in the way such distance is computed. In order to exploit the effectiveness of the different methods in capturing distinct properties of data distributions and, accordingly, efficiently tackle the trade-off between generalization and overfitting, EAD employs detector-specific distance scores as features of a logistic regression classifier, after independent hyperparameters optimization. We evaluated the EAD approach on distinct datasets (CIFAR-10, CIFAR-100 and SVHN) and models (ResNet and DenseNet) and with regard to four adversarial attacks (FGSM, BIM, DeepFool and CW), also by comparing with competing approaches. Overall, we show that EAD achieves the best AUROC and AUPR in the large majority of the settings and comparable performance in the others. The improvement over the state-of-the-art, and the possibility to easily extend EAD to include any arbitrary set of detectors, pave the way to a widespread adoption of ensemble approaches in the broad field of adversarial example detection.
Investigating the Compositional Structure Of Deep Neural Networks
Feb 17, 2020



Abstract:The current understanding of deep neural networks can only partially explain how input structure, network parameters and optimization algorithms jointly contribute to achieve the strong generalization power that is typically observed in many real-world applications. In order to improve the comprehension and interpretability of deep neural networks, we here introduce a novel theoretical framework based on the compositional structure of piecewise linear activation functions. By defining a direct acyclic graph representing the composition of activation patterns through the network layers, it is possible to characterize the instances of the input data with respect to both the predicted label and the specific (linear) transformation used to perform predictions. Preliminary tests on the MNIST dataset show that our method can group input instances with regard to their similarity in the internal representation of the neural network, providing an intuitive measure of input complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge