The Ultimate Combo: Boosting Adversarial Example Transferability by Composing Data Augmentations

Transferring adversarial examples (AEs) from surrogate machine-learning (ML) models to target models is commonly used in black-box adversarial robustness evaluation. Attacks leveraging certain data augmentation, such as random resizing, have been found to help AEs generalize from surrogates to targets. Yet, prior work has explored limited augmentations and their composition. To fill the gap, we systematically studied how data augmentation affects transferability. Particularly, we explored 46 augmentation techniques of seven categories originally proposed to help ML models generalize to unseen benign samples, and assessed how they impact transferability, when applied individually or composed. Performing exhaustive search on a small subset of augmentation techniques and genetic search on all techniques, we identified augmentation combinations that can help promote transferability. Extensive experiments with the ImageNet and CIFAR-10 datasets and 18 models showed that simple color-space augmentations (e.g., color to greyscale) outperform the state of the art when combined with standard augmentations, such as translation and scaling. Additionally, we discovered that composing augmentations impacts transferability mostly monotonically (i.e., more methods composed $\rightarrow$ $\ge$ transferability). We also found that the best composition significantly outperformed the state of the art (e.g., 93.7% vs. $\le$ 82.7% average transferability on ImageNet from normally trained surrogates to adversarially trained targets). Lastly, our theoretical analysis, backed up by empirical evidence, intuitively explain why certain augmentations help improve transferability.

A Simple Explanation for the Existence of Adversarial Examples with Small Hamming Distance

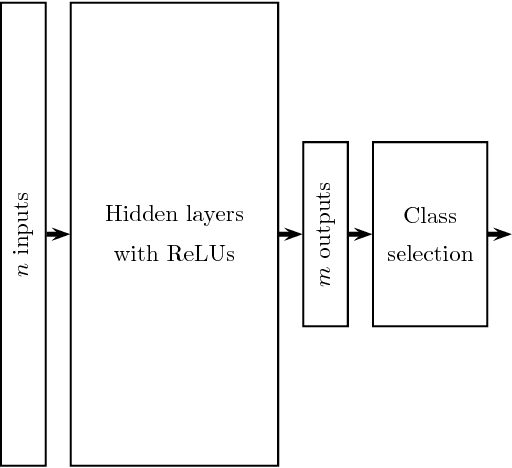
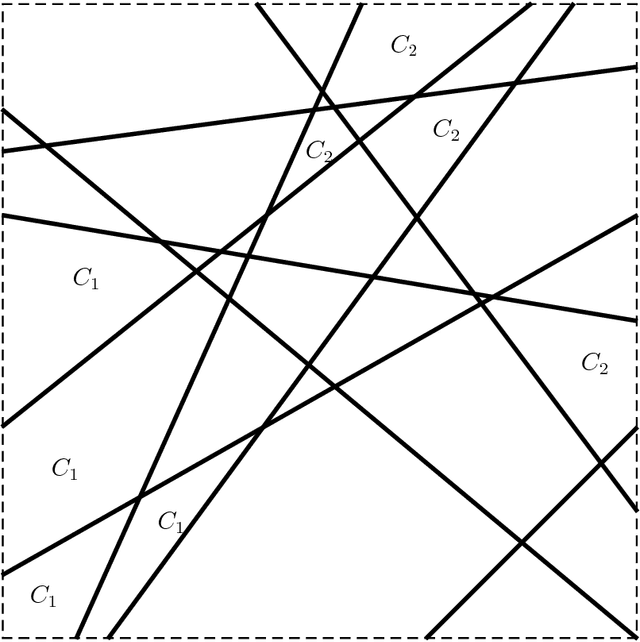
The existence of adversarial examples in which an imperceptible change in the input can fool well trained neural networks was experimentally discovered by Szegedy et al in 2013, who called them "Intriguing properties of neural networks". Since then, this topic had become one of the hottest research areas within machine learning, but the ease with which we can switch between any two decisions in targeted attacks is still far from being understood, and in particular it is not clear which parameters determine the number of input coordinates we have to change in order to mislead the network. In this paper we develop a simple mathematical framework which enables us to think about this baffling phenomenon from a fresh perspective, turning it into a natural consequence of the geometry of $\mathbb{R}^n$ with the $L_0$ (Hamming) metric, which can be quantitatively analyzed. In particular, we explain why we should expect to find targeted adversarial examples with Hamming distance of roughly $m$ in arbitrarily deep neural networks which are designed to distinguish between $m$ input classes.