miniCodeProps: a Minimal Benchmark for Proving Code Properties

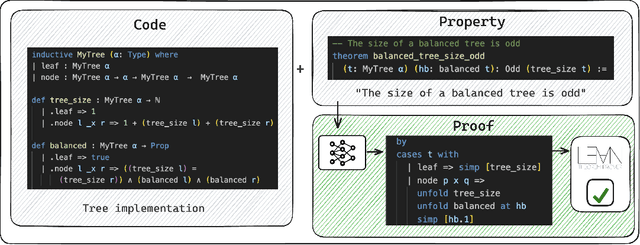
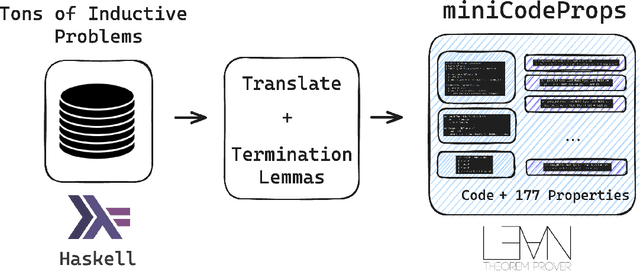
Neural networks have shown initial promise in automating mathematical theorem proving in proof assistants such as Lean. The same proof assistants can be used to verify the correctness of code by pairing code with specifications and proofs that the specifications hold. Automating the writing of code, specifications, and proofs could lower the cost of verification, or, ambitiously, enable a machine learning system to output provably correct code. However, it remains unclear whether current neural theorem provers can automatically verify even relatively simple programs. We present miniCodeProps, a benchmark of 177 program specifications in the Lean proof assistant, aimed at the subproblem of automatically generating a proof for a provided program and specification. miniCodeProps contains specifications about simple, self-contained programs (e.g., lists, natural numbers, binary trees) with varied proof difficulty. Despite its simplicity, miniCodeProps is challenging for current LLM-based provers, which succeed in proving about 25 percent of the specifications. We publicly release miniCodeProps as a benchmark for furthering automated theorem proving in the context of formally verified code.

Compression with Flows via Local Bits-Back Coding

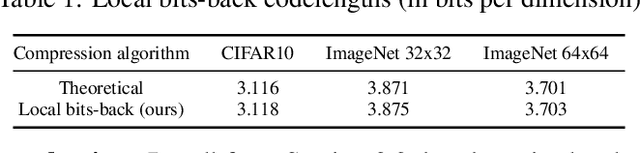
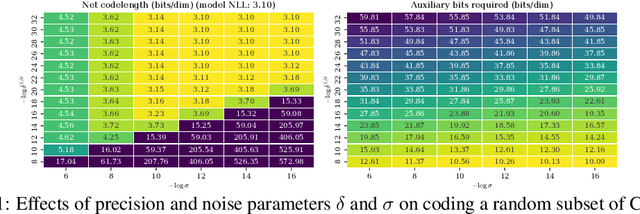
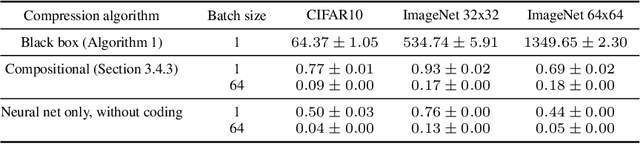
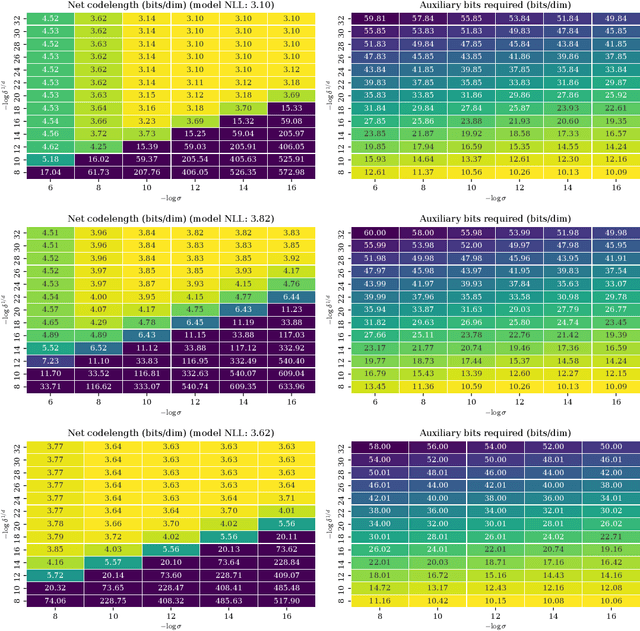
Likelihood-based generative models are the backbones of lossless compression, due to the guaranteed existence of codes with lengths close to negative log likelihood. However, there is no guaranteed existence of computationally efficient codes that achieve these lengths, and coding algorithms must be hand-tailored to specific types of generative models to ensure computational efficiency. Such coding algorithms are known for autoregressive models and variational autoencoders, but not for general types of flow models. To fill in this gap, we introduce local bits-back coding, a new compression technique compatible with flow models. We present efficient algorithms that instantiate our technique for many popular types of flows, and we demonstrate that our algorithms closely achieve theoretical codelengths for state-of-the-art flow models on high-dimensional data.