Linear Least Squares Estimation of Fiber-Longitudinal Optical Power Profile

This paper presents a linear least squares method for fiber-longitudinal power profile estimation (PPE), which estimates an optical signal power distribution throughout a fiber-optic link at a coherent receiver. The method finds the global optimum in least square estimation of longitudinal power profiles, thus closely matching true optical power profiles and locating loss anomalies in a link with high spatial resolution. Experimental results show that the method achieves accurate PPE with an RMS error from OTDR of 0.18 dB. Consequently, it successfully identifies a loss anomaly as small as 0.77 dB, demonstrating the potential of a coherent receiver in locating even splice and connector losses. The method is also evaluated under a WDM condition with optimal system fiber launch power, highlighting its feasibility for use in operations. Furthermore, a fundamental limit for stable estimation and spatial resolution of least-squares-based PPE is quantitatively discussed in relation to the ill-posedness of PPE by evaluating the condition number of a nonlinear perturbation matrix.

Performance limit of Fiber-Longitudinal Power Profile Estimation Methods

This paper presents analytical results on power profile estimation (PPE) methods, which visualize a signal power evolution in the fiber-longitudinal direction at a coherent receiver. Two types of PPE methods are reviewed and analyzed, including correlation-based methods (CMs) and minimum-mean-square-error-based methods (MMSEs). The analytical expressions for their output power profiles and spatial resolution are provided, and thus the theoretical performance limits of the two PPE methods and their differences are clarified. The derived equations indicate that the estimated power profiles of CMs can be understood as the convolution of a true power profile and a smoothing function. Thus, the spatial resolution and measurement accuracy of CMs are limited, even under noiseless and distortionless conditions. Based on this fact, closed-form formulas for the spatial resolution of CMs are presented. On the other hand, in MMSEs, such a convolution effect is canceled out and thus the estimated power profiles approach a true power profile under a fine spatial step size.

Physics-oriented learning of nonlinear Schrödinger equation: optical fiber loss and dispersion profile identification

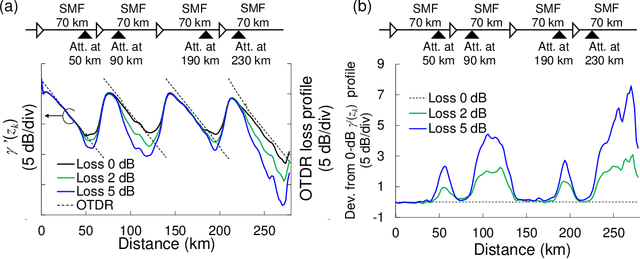
In optical fiber communication, system identification (SI) for the nonlinear Schr\"odinger equation (NLSE) has long been studied mainly for fiber nonlinearity compensation (NLC). One recent line of inquiry to combine a behavioral-model approach like digital backpropagation (DBP) and a data-driven approach like neural network (NN). These works are aimed for more NLC gain; however, by directing our attention to the learned parameters in such a SI process, system status information, i.e., optical fiber parameters, will possibly be extracted. Here, we show that the model-based optimization and interpretable nature of the learned parameters in NN-based DBP enable transmission line monitoring, fully extracting the actual in-line NLSE parameter distributions. Specifically, we demonstrate that longitudinal loss and dispersion profiles along a multi-span link can be obtained at once, directly from data-carrying signals without any dedicated analog devices such as optical time-domain reflectometry. We apply the method to a long-haul (~2,080 km) link and various link conditions are tested, including excess loss inserted, different fiber input power, and non-uniform level diagram. The measurement performance is also investigated in terms of measurement range, accuracy, and fiber launch power. These results provide a path toward simplified and automated network management as another application of DBP.