Ethan Sequeira
Towards Optimal Beacon Placement for Range-Aided Localization
May 19, 2024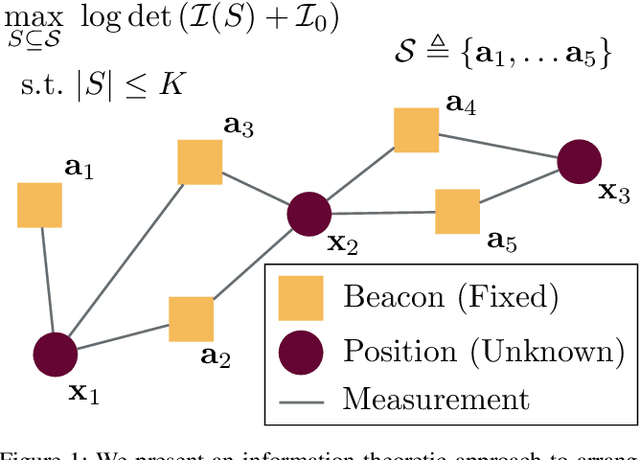
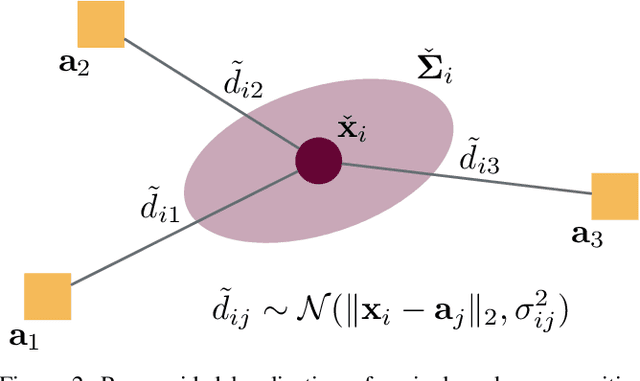

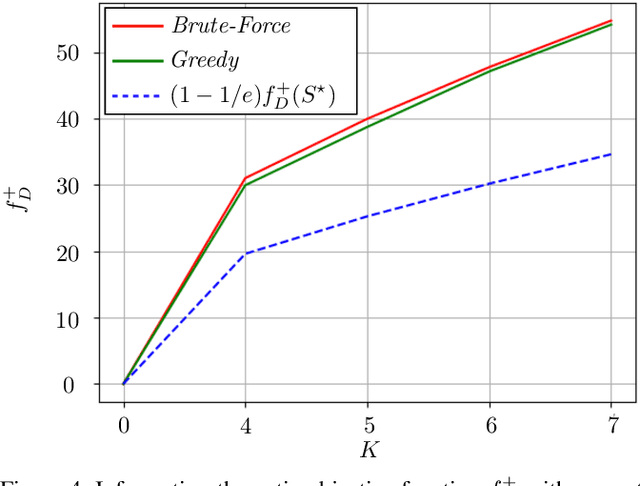
Abstract:Range-based localization is ubiquitous: global navigation satellite systems (GNSS) power mobile phone-based navigation, and autonomous mobile robots can use range measurements from a variety of modalities including sonar, radar, and even WiFi signals. Many of these localization systems rely on fixed anchors or beacons with known positions acting as transmitters or receivers. In this work, we answer a fundamental question: given a set of positions we would like to localize, how should beacons be placed so as to minimize localization error? Specifically, we present an information theoretic method for optimally selecting an arrangement consisting of a few beacons from a large set of candidate positions. By formulating localization as maximum a posteriori (MAP) estimation, we can cast beacon arrangement as a submodular set function maximization problem. This approach is probabilistically rigorous, simple to implement, and extremely flexible. Furthermore, we prove that the submodular structure of our problem formulation ensures that a greedy algorithm for beacon arrangement has suboptimality guarantees. We compare our method with a number of benchmarks on simulated data and release an open source Python implementation of our algorithm and experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge