Controllable Quantum Memory Capacity in Quantum Reservoir Networks with Tunable partial-SWAPs

In the field of quantum reservoir computing (QRC), many different computational models and architectures have been proposed. From these models, we identify feedback based models -- which use a feedback mechanism to re-embed classical measurements from the QRC -- and recurrent models -- which use a multi-register approach with memory and readout qubits -- as the two major competing architectures that have been discussed and validated on hardware. In this paper, we advance upon the recurrent architectures, which employ a two register approach to endow the QRC with a fading memory. While these approaches have been validated on hardware and have demonstrated great real-world performance on noisy-intermediate-scale-quantum (NISQ) quantum processing units (QPUs), the exact mechanism through which the memory capacity arises is not completely understood or fully controllable. With this, we augment the recurrent approaches and present a hardware-realizable mechanism, which we call a tunable partial-SWAP, that allows for the direct control of the rate of memory dissipation from a QRN implemented on a gate-based QPU. The theory behind this mechanism is discussed in terms of a controlled amplitude-damping channel and validation experiments using a randomized short-term memory capacity (STMC) recall benchmark and the NARMA-5 dataset are conducted using simulation and IBM QPUs, respectively.

Quantum Observers: A NISQ Hardware Demonstration of Chaotic State Prediction Using Quantum Echo-state Networks

Recent advances in artificial intelligence have highlighted the remarkable capabilities of neural network (NN)-powered systems on classical computers. However, these systems face significant computational challenges that limit scalability and efficiency. Quantum computers hold the potential to overcome these limitations and increase processing power beyond classical systems. Despite this, integrating quantum computing with NNs remains largely unrealized due to challenges posed by noise, decoherence, and high error rates in current quantum hardware. Here, we propose a novel quantum echo-state network (QESN) design and implementation algorithm that can operate within the presence of noise on current IBM hardware. We apply classical control-theoretic response analysis to characterize the QESN, emphasizing its rich nonlinear dynamics and memory, as well as its ability to be fine-tuned with sparsity and re-uploading blocks. We validate our approach through a comprehensive demonstration of QESNs functioning as quantum observers, applied in both high-fidelity simulations and hardware experiments utilizing data from a prototypical chaotic Lorenz system. Our results show that the QESN can predict long time-series with persistent memory, running over 100 times longer than the median T}1 and T2 of the IBM Marrakesh QPU, achieving state-of-the-art time-series performance on superconducting hardware.

Learning with SASQuaTCh: a Novel Variational Quantum Transformer Architecture with Kernel-Based Self-Attention

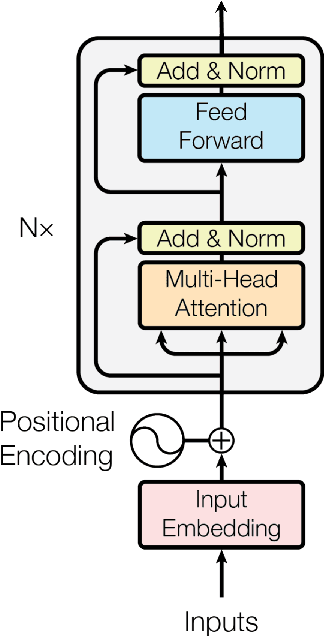
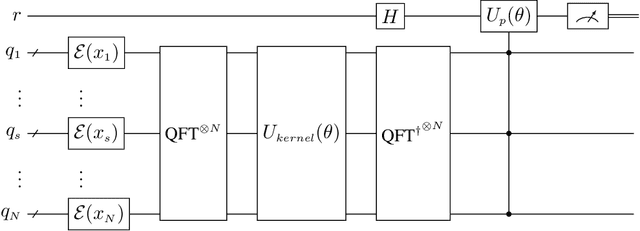
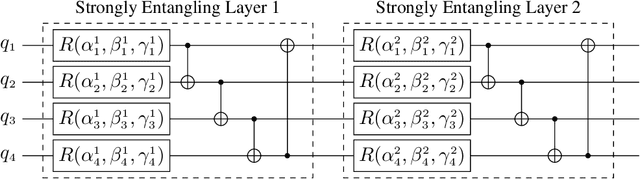
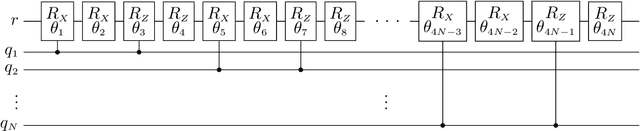
The widely popular transformer network popularized by the generative pre-trained transformer (GPT) has a large field of applicability, including predicting text and images, classification, and even predicting solutions to the dynamics of physical systems. In the latter context, the continuous analog of the self-attention mechanism at the heart of transformer networks has been applied to learning the solutions of partial differential equations and reveals a convolution kernel nature that can be exploited by the Fourier transform. It is well known that many quantum algorithms that have provably demonstrated a speedup over classical algorithms utilize the quantum Fourier transform. In this work, we explore quantum circuits that can efficiently express a self-attention mechanism through the perspective of kernel-based operator learning. In this perspective, we are able to represent deep layers of a vision transformer network using simple gate operations and a set of multi-dimensional quantum Fourier transforms. We analyze the computational and parameter complexity of our novel variational quantum circuit, which we call Self-Attention Sequential Quantum Transformer Channel (SASQuaTCh), and demonstrate its utility on simplified classification problems.

A Quick Introduction to Quantum Machine Learning for Non-Practitioners

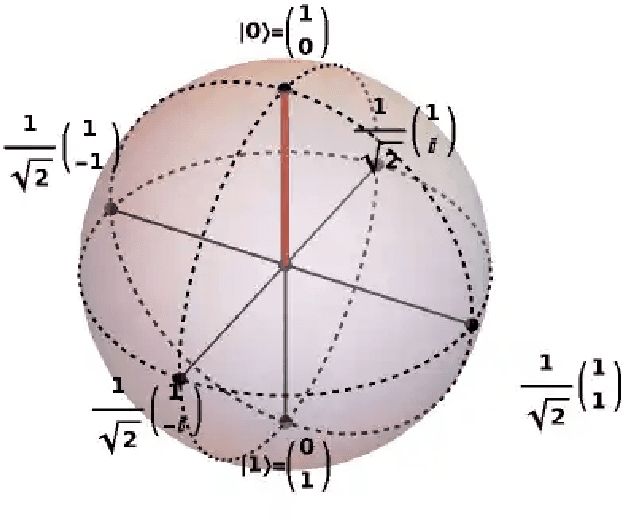
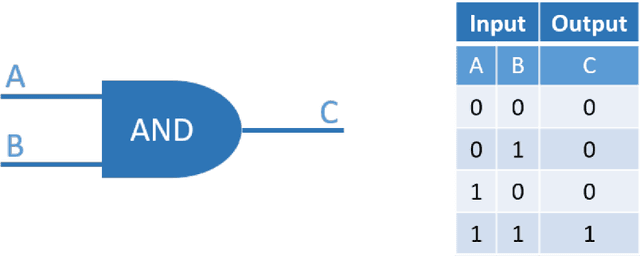
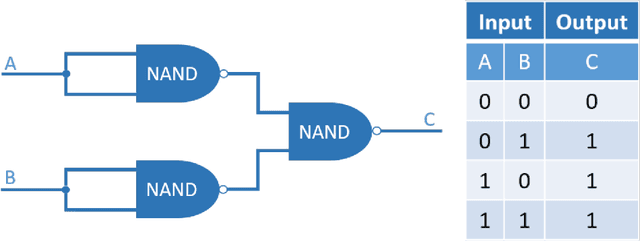
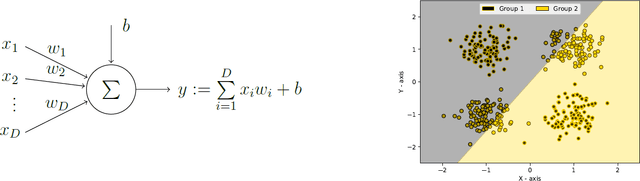
This paper provides an introduction to quantum machine learning, exploring the potential benefits of using quantum computing principles and algorithms that may improve upon classical machine learning approaches. Quantum computing utilizes particles governed by quantum mechanics for computational purposes, leveraging properties like superposition and entanglement for information representation and manipulation. Quantum machine learning applies these principles to enhance classical machine learning models, potentially reducing network size and training time on quantum hardware. The paper covers basic quantum mechanics principles, including superposition, phase space, and entanglement, and introduces the concept of quantum gates that exploit these properties. It also reviews classical deep learning concepts, such as artificial neural networks, gradient descent, and backpropagation, before delving into trainable quantum circuits as neural networks. An example problem demonstrates the potential advantages of quantum neural networks, and the appendices provide detailed derivations. The paper aims to help researchers new to quantum mechanics and machine learning develop their expertise more efficiently.

Stochastic Spatio-Temporal Optimization for Control and Co-Design of Systems in Robotics and Applied Physics

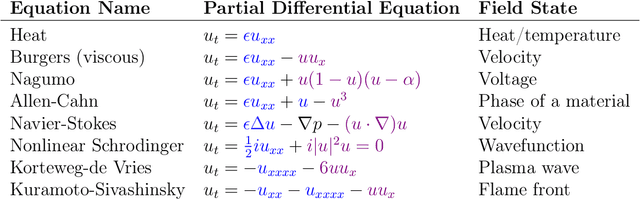
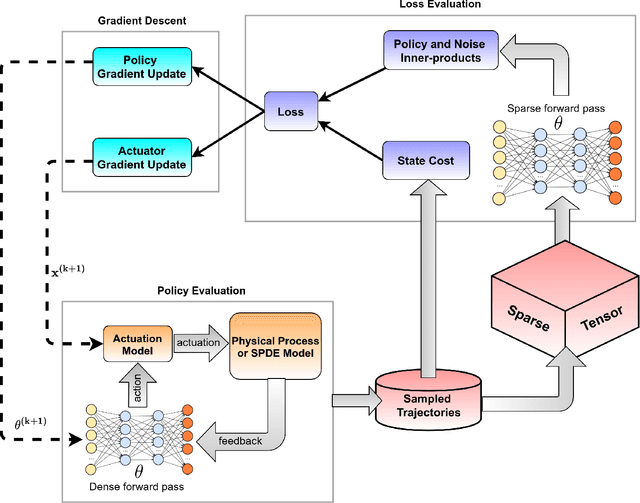
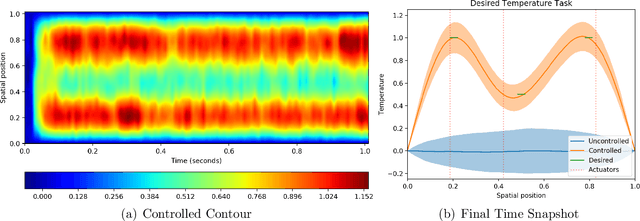
Correlated with the trend of increasing degrees of freedom in robotic systems is a similar trend of rising interest in Spatio-Temporal systems described by Partial Differential Equations (PDEs) among the robotics and control communities. These systems often exhibit dramatic under-actuation, high dimensionality, bifurcations, and multimodal instabilities. Their control represents many of the current-day challenges facing the robotics and automation communities. Not only are these systems challenging to control, but the design of their actuation is an NP-hard problem on its own. Recent methods either discretize the space before optimization, or apply tools from linear systems theory under restrictive linearity assumptions in order to arrive at a control solution. This manuscript provides a novel sampling-based stochastic optimization framework based entirely in Hilbert spaces suitable for the general class of \textit{semi-linear} SPDEs which describes many systems in robotics and applied physics. This framework is utilized for simultaneous policy optimization and actuator co-design optimization. The resulting algorithm is based on variational optimization, and performs joint episodic optimization of the feedback control law and the actuation design over episodes. We study first and second order systems, and in doing so, extend several results to the case of second order SPDEs. Finally, we demonstrate the efficacy of the proposed approach with several simulated experiments on a variety of SPDEs in robotics and applied physics including an infinite degree-of-freedom soft robotic manipulator.