Espen Bernton
Schrödinger Bridge Samplers
Dec 31, 2019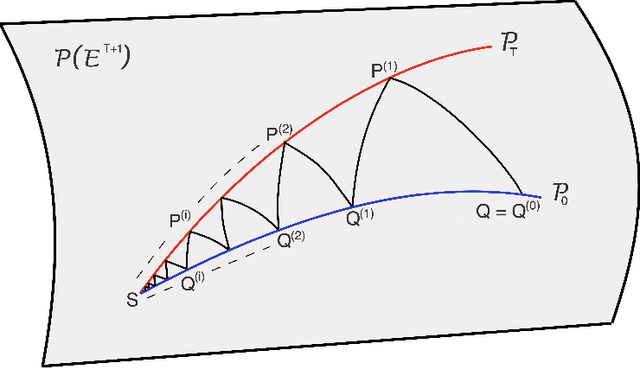
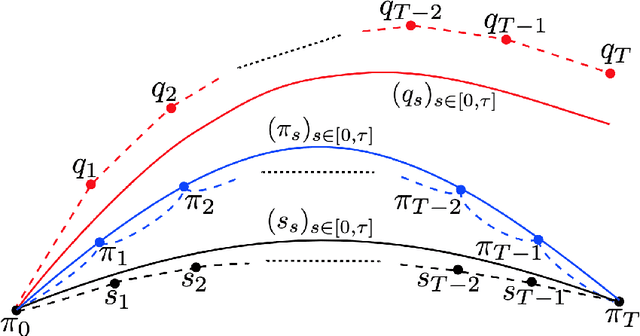
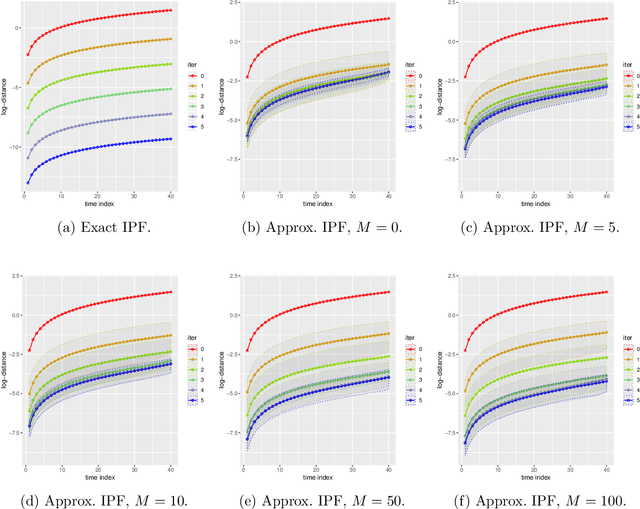
Abstract:Consider a reference Markov process with initial distribution $\pi_{0}$ and transition kernels $\{M_{t}\}_{t\in[1:T]}$, for some $T\in\mathbb{N}$. Assume that you are given distribution $\pi_{T}$, which is not equal to the marginal distribution of the reference process at time $T$. In this scenario, Schr\"odinger addressed the problem of identifying the Markov process with initial distribution $\pi_{0}$ and terminal distribution equal to $\pi_{T}$ which is the closest to the reference process in terms of Kullback--Leibler divergence. This special case of the so-called Schr\"odinger bridge problem can be solved using iterative proportional fitting, also known as the Sinkhorn algorithm. We leverage these ideas to develop novel Monte Carlo schemes, termed Schr\"odinger bridge samplers, to approximate a target distribution $\pi$ on $\mathbb{R}^{d}$ and to estimate its normalizing constant. This is achieved by iteratively modifying the transition kernels of the reference Markov chain to obtain a process whose marginal distribution at time $T$ becomes closer to $\pi_T = \pi$, via regression-based approximations of the corresponding iterative proportional fitting recursion. We report preliminary experiments and make connections with other problems arising in the optimal transport, optimal control and physics literatures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge