Graph Matching via convex relaxation to the simplex

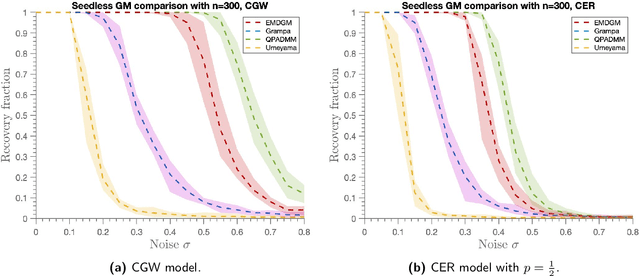
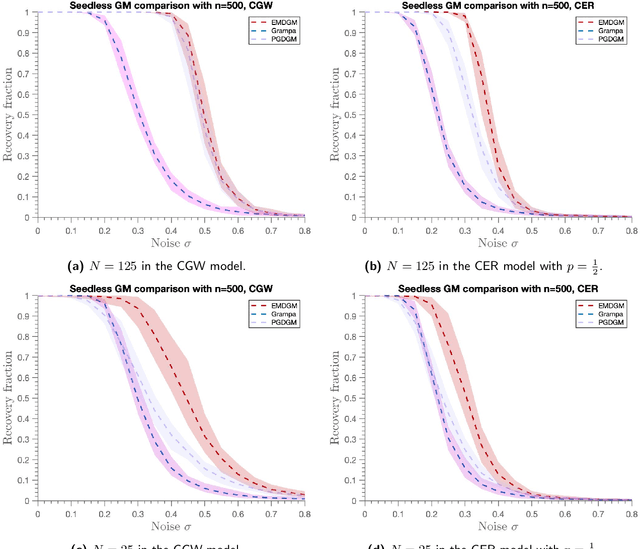
This paper addresses the Graph Matching problem, which consists of finding the best possible alignment between two input graphs, and has many applications in computer vision, network deanonymization and protein alignment. A common approach to tackle this problem is through convex relaxations of the NP-hard \emph{Quadratic Assignment Problem} (QAP). Here, we introduce a new convex relaxation onto the unit simplex and develop an efficient mirror descent scheme with closed-form iterations for solving this problem. Under the correlated Gaussian Wigner model, we show that the simplex relaxation admits a unique solution with high probability. In the noiseless case, this is shown to imply exact recovery of the ground truth permutation. Additionally, we establish a novel sufficiency condition for the input matrix in standard greedy rounding methods, which is less restrictive than the commonly used `diagonal dominance' condition. We use this condition to show exact one-step recovery of the ground truth (holding almost surely) via the mirror descent scheme, in the noiseless setting. We also use this condition to obtain significantly improved conditions for the GRAMPA algorithm [Fan et al. 2019] in the noiseless setting.

Random Geometric Graphs on Euclidean Balls

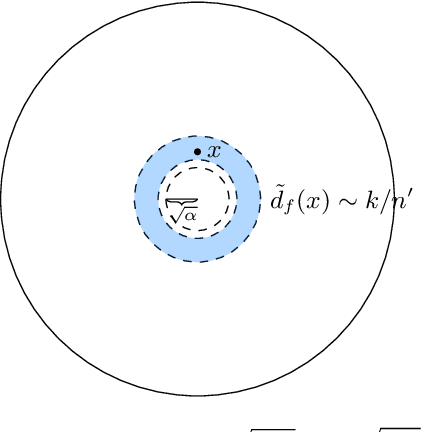
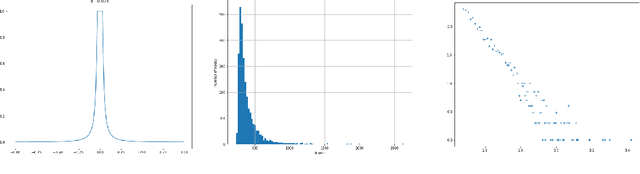
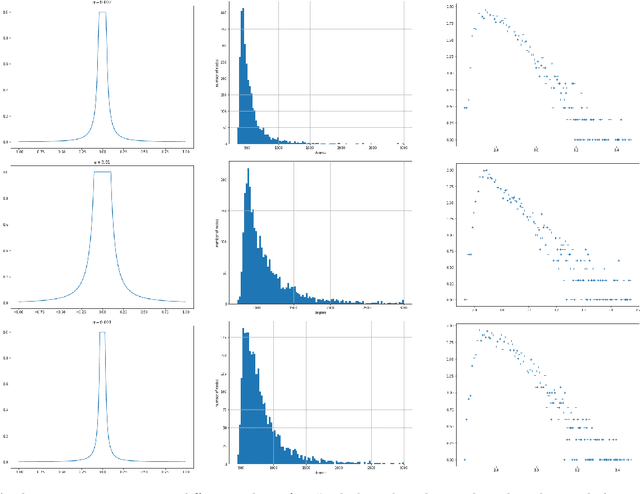
We consider a latent space model for random graphs where a node $i$ is associated to a random latent point $X_i$ on the Euclidean unit ball. The probability that an edge exists between two nodes is determined by a ``link'' function, which corresponds to a dot product kernel. For a given class $\F$ of spherically symmetric distributions for $X_i$, we consider two estimation problems: latent norm recovery and latent Gram matrix estimation. We construct an estimator for the latent norms based on the degree of the nodes of an observed graph in the case of the model where the edge probability is given by $f(\langle X_i,X_j\rangle)=\mathbbm{1}_{\langle X_i,X_j\rangle\geq \tau}$, where $0<\tau<1$. We introduce an estimator for the Gram matrix based on the eigenvectors of observed graph and we establish Frobenius type guarantee for the error, provided that the link function is sufficiently regular in the Sobolev sense and that a spectral-gap-type condition holds. We prove that for certain link functions, the model considered here generates graphs with degree distribution that have tails with a power-law-type distribution, which can be seen as an advantage of the model presented here with respect to the classic Random Geometric Graph model on the Euclidean sphere. We illustrate our results with numerical experiments.

Relative concentration bounds for the kernel matrix spectrum

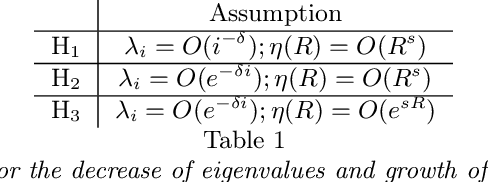
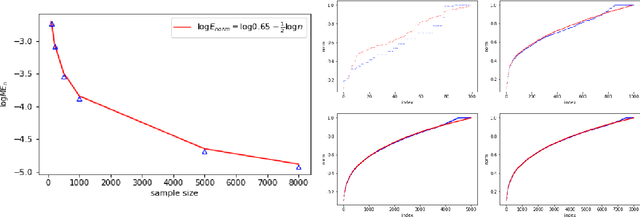
In this paper, we study the concentration properties of the kernel matrix associated to a kernel function. Specifically, we derive new concentration inequalities for the spectrum of an kernel matrix, quantifying its deviation with respect to an associated integral operator. The main difference with most results in the literature is that we do not assume the positive definiteness of the kernel. Instead, we introduce Sobolev type hypothesis on the regularity of the kernel. We show how this is well suited to the study of kernels depending only on the distance between two points in a metric space, in which case the regularity depends only on the decay of the eigenvalues. This is connected with geometric random graphs, which we study further, exhibiting explicit formulas for the spectrum and its fluctuation.