Relative concentration bounds for the kernel matrix spectrum

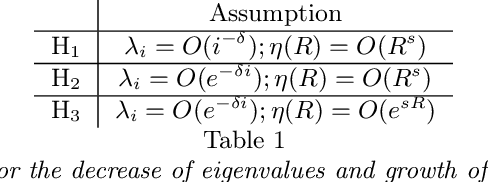
In this paper, we study the concentration properties of the kernel matrix associated to a kernel function. Specifically, we derive new concentration inequalities for the spectrum of an kernel matrix, quantifying its deviation with respect to an associated integral operator. The main difference with most results in the literature is that we do not assume the positive definiteness of the kernel. Instead, we introduce Sobolev type hypothesis on the regularity of the kernel. We show how this is well suited to the study of kernels depending only on the distance between two points in a metric space, in which case the regularity depends only on the decay of the eigenvalues. This is connected with geometric random graphs, which we study further, exhibiting explicit formulas for the spectrum and its fluctuation.