Random Geometric Graphs on Euclidean Balls
Paper and Code
Oct 26, 2020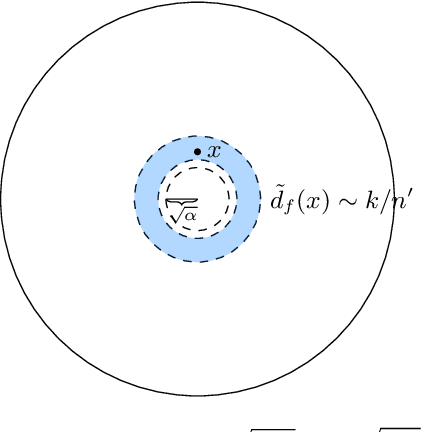
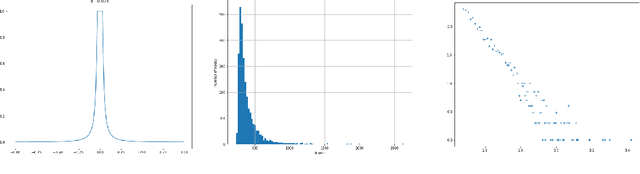
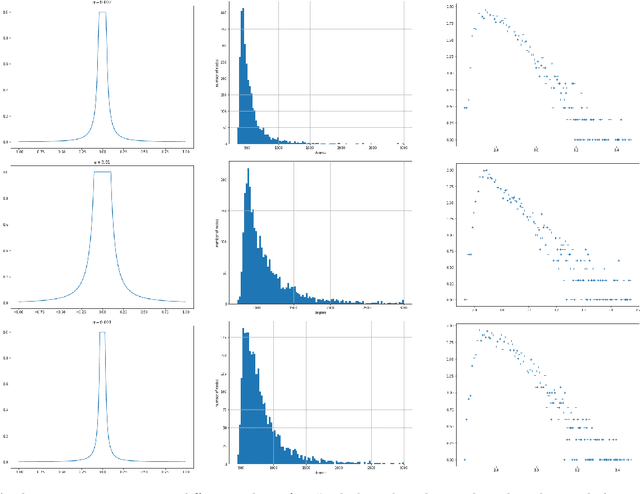
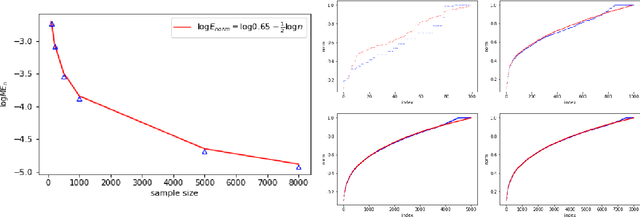
We consider a latent space model for random graphs where a node $i$ is associated to a random latent point $X_i$ on the Euclidean unit ball. The probability that an edge exists between two nodes is determined by a ``link'' function, which corresponds to a dot product kernel. For a given class $\F$ of spherically symmetric distributions for $X_i$, we consider two estimation problems: latent norm recovery and latent Gram matrix estimation. We construct an estimator for the latent norms based on the degree of the nodes of an observed graph in the case of the model where the edge probability is given by $f(\langle X_i,X_j\rangle)=\mathbbm{1}_{\langle X_i,X_j\rangle\geq \tau}$, where $0<\tau<1$. We introduce an estimator for the Gram matrix based on the eigenvectors of observed graph and we establish Frobenius type guarantee for the error, provided that the link function is sufficiently regular in the Sobolev sense and that a spectral-gap-type condition holds. We prove that for certain link functions, the model considered here generates graphs with degree distribution that have tails with a power-law-type distribution, which can be seen as an advantage of the model presented here with respect to the classic Random Geometric Graph model on the Euclidean sphere. We illustrate our results with numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge