Autobahn: Automorphism-based Graph Neural Nets

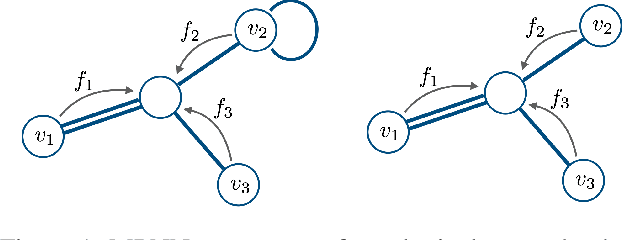
We introduce Automorphism-based graph neural networks (Autobahn), a new family of graph neural networks. In an Autobahn, we decompose the graph into a collection of subgraphs and applying local convolutions that are equivariant to each subgraph's automorphism group. Specific choices of local neighborhoods and subgraphs recover existing architectures such as message passing neural networks. However, our formalism also encompasses novel architectures: as an example, we introduce a graph neural network that decomposes the graph into paths and cycles. The resulting convolutions reflect the natural way that parts of the graph can transform, preserving the intuitive meaning of convolution without sacrificing global permutation equivariance. We validate our approach by applying Autobahn to molecular graphs, where it achieves state-of-the-art results.

The general theory of permutation equivarant neural networks and higher order graph variational encoders

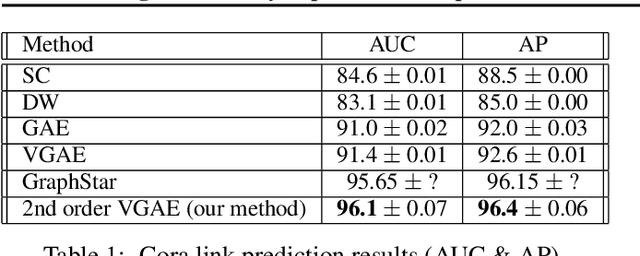
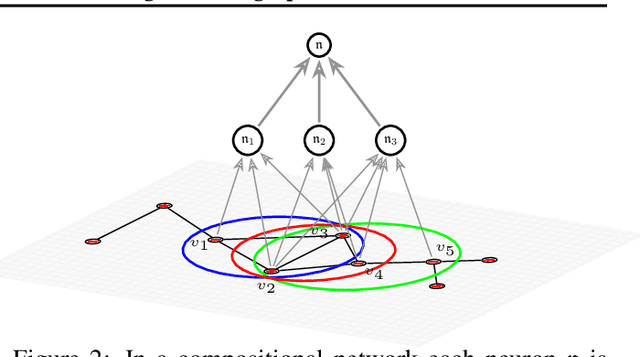
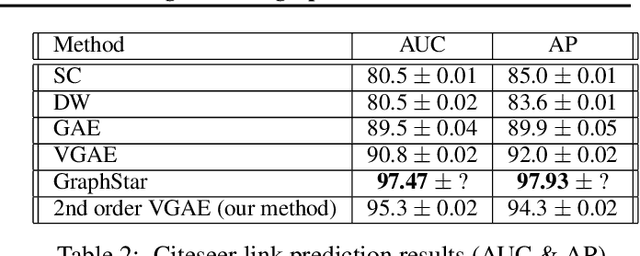
Previous work on symmetric group equivariant neural networks generally only considered the case where the group acts by permuting the elements of a single vector. In this paper we derive formulae for general permutation equivariant layers, including the case where the layer acts on matrices by permuting their rows and columns simultaneously. This case arises naturally in graph learning and relation learning applications. As a specific case of higher order permutation equivariant networks, we present a second order graph variational encoder, and show that the latent distribution of equivariant generative models must be exchangeable. We demonstrate the efficacy of this architecture on the tasks of link prediction in citation graphs and molecular graph generation.