Physics-based machine learning for modeling stochastic IP3-dependent calcium dynamics

We present a machine learning method for model reduction which incorporates domain-specific physics through candidate functions. Our method estimates an effective probability distribution and differential equation model from stochastic simulations of a reaction network. The close connection between reduced and fine scale descriptions allows approximations derived from the master equation to be introduced into the learning problem. This representation is shown to improve generalization and allows a large reduction in network size for a classic model of inositol trisphosphate (IP3) dependent calcium oscillations in non-excitable cells.

Diff2Dist: Learning Spectrally Distinct Edge Functions, with Applications to Cell Morphology Analysis

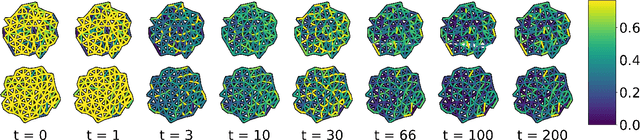
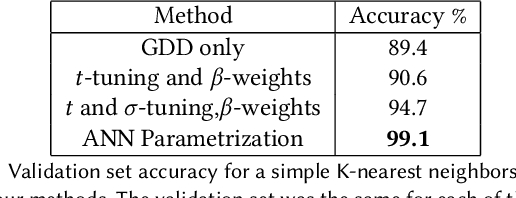
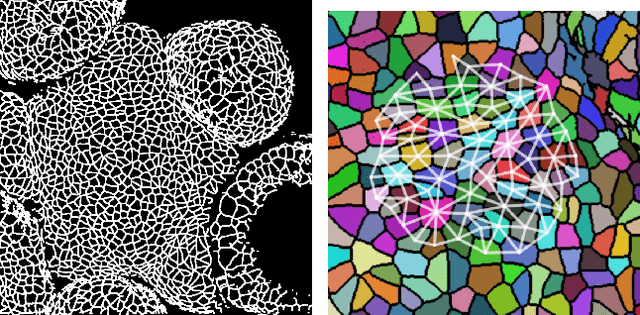
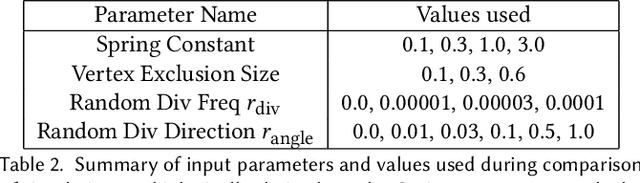
We present a method for learning "spectrally descriptive" edge weights for graphs. We generalize a previously known distance measure on graphs (Graph Diffusion Distance), thereby allowing it to be tuned to minimize an arbitrary loss function. Because all steps involved in calculating this modified GDD are differentiable, we demonstrate that it is possible for a small neural network model to learn edge weights which minimize loss. GDD alone does not effectively discriminate between graphs constructed from shoot apical meristem images of wild-type vs. mutant \emph{Arabidopsis thaliana} specimens. However, training edge weights and kernel parameters with contrastive loss produces a learned distance metric with large margins between these graph categories. We demonstrate this by showing improved performance of a simple k-nearest-neighbors classifier on the learned distance matrix. We also demonstrate a further application of this method to biological image analysis: once trained, we use our model to compute the distance between the biological graphs and a set of graphs output by a cell division simulator. This allows us to identify simulation parameter regimes which are similar to each class of graph in our original dataset.

Graph Prolongation Convolutional Networks: Explicitly Multiscale Machine Learning on Graphs, with Applications to Modeling of Biological Systems

We define a novel type of ensemble Graph Convolutional Network (GCN) model. Using optimized linear projection operators to map between spatial scales of graph, this ensemble model learns to aggregate information from each scale for its final prediction. We calculate these linear projection operators as the infima of an objective function relating the structure matrices used for each GCN. Equipped with these projections, our model (a Graph Prolongation-Convolutional Network) outperforms other GCN ensemble models at predicting the potential energy of monomer subunits in a coarse-grained mechanochemical simulation of microtubule bending. We demonstrate these performance gains by measuring an estimate of the FLOPs spent to train each model, as well as wall-clock time. Because our model learns at multiple scales, it is possible to train at each scale according to a predetermined schedule of coarse vs. fine training. We examine several such schedules adapted from the Algebraic Multigrid (AMG) literature, and quantify the computational benefit of each. Finally, we demonstrate how under certain assumptions, our graph prolongation layers may be decomposed into a matrix outer product of smaller GCN operations.

Novel diffusion-derived distance measures for graphs

We define a new family of similarity and distance measures on graphs, and explore their theoretical properties in comparison to conventional distance metrics. These measures are defined by the solution(s) to an optimization problem which attempts find a map minimizing the discrepancy between two graph Laplacian exponential matrices, under norm-preserving and sparsity constraints. Variants of the distance metric are introduced to consider such optimized maps under sparsity constraints as well as fixed time-scaling between the two Laplacians. The objective function of this optimization is multimodal and has discontinuous slope, and is hence difficult for univariate optimizers to solve. We demonstrate a novel procedure for efficiently calculating these optima for two of our distance measure variants. We present numerical experiments demonstrating that (a) upper bounds of our distance metrics can be used to distinguish between lineages of related graphs; (b) our procedure is faster at finding the required optima, by as much as a factor of 10^3; and (c) the upper bounds satisfy the triangle inequality exactly under some assumptions and approximately under others. We also derive an upper bound for the distance between two graph products, in terms of the distance between the two pairs of factors. Additionally, we present several possible applications, including the construction of infinite "graph limits" by means of Cauchy sequences of graphs related to one another by our distance measure.

Deep Learning Moment Closure Approximations using Dynamic Boltzmann Distributions

The moments of spatial probabilistic systems are often given by an infinite hierarchy of coupled differential equations. Moment closure methods are used to approximate a subset of low order moments by terminating the hierarchy at some order and replacing higher order terms with functions of lower order ones. For a given system, it is not known beforehand which closure approximation is optimal, i.e. which higher order terms are relevant in the current regime. Further, the generalization of such approximations is typically poor, as higher order corrections may become relevant over long timescales. We have developed a method to learn moment closure approximations directly from data using dynamic Boltzmann distributions (DBDs). The dynamics of the distribution are parameterized using basis functions from finite element methods, such that the approach can be applied without knowing the true dynamics of the system under consideration. We use the hierarchical architecture of deep Boltzmann machines (DBMs) with multinomial latent variables to learn closure approximations for progressively higher order spatial correlations. The learning algorithm uses a centering transformation, allowing the dynamic DBM to be trained without the need for pre-training. We demonstrate the method for a Lotka-Volterra system on a lattice, a typical example in spatial chemical reaction networks. The approach can be applied broadly to learn deep generative models in applications where infinite systems of differential equations arise.

Multilevel Artificial Neural Network Training for Spatially Correlated Learning

Multigrid modeling algorithms are a technique used to accelerate relaxation models running on a hierarchy of similar graphlike structures. We introduce and demonstrate a new method for training neural networks which uses multilevel methods. Using an objective function derived from a graph-distance metric, we perform orthogonally-constrained optimization to find optimal prolongation and restriction maps between graphs. We compare and contrast several methods for performing this numerical optimization, and additionally present some new theoretical results on upper bounds of this type of objective function. Once calculated, these optimal maps between graphs form the core of Multiscale Artificial Neural Network (MsANN) training, a new procedure we present which simultaneously trains a hierarchy of neural network models of varying spatial resolution. Parameter information is passed between members of this hierarchy according to standard coarsening and refinement schedules from the multiscale modelling literature. In our machine learning experiments, these models are able to learn faster than default training, achieving a comparable level of error in an order of magnitude fewer training examples.

Prospects for Declarative Mathematical Modeling of Complex Biological Systems

Declarative modeling uses symbolic expressions to represent models. With such expressions one can formalize high-level mathematical computations on models that would be difficult or impossible to perform directly on a lower-level simulation program, in a general-purpose programming language. Examples of such computations on models include model analysis, relatively general-purpose model-reduction maps, and the initial phases of model implementation, all of which should preserve or approximate the mathematical semantics of a complex biological model. Multiscale modeling benefits from both the expressive power of declarative modeling languages and the application of model reduction methods to link models across scale. Based on previous work, here we define declarative modeling of complex biological systems by defining the semantics of an increasingly powerful series of declarative modeling languages including reaction-like dynamics of parameterized and extended objects, we define semantics-preserving implementation and semantics-approximating model reduction transformations, and we outline a "meta-hierarchy" for organizing declarative models and the mathematical methods that can fruitfully manipulate them.

Compositional Stochastic Modeling and Probabilistic Programming

Probabilistic programming is related to a compositional approach to stochastic modeling by switching from discrete to continuous time dynamics. In continuous time, an operator-algebra semantics is available in which processes proceeding in parallel (and possibly interacting) have summed time-evolution operators. From this foundation, algorithms for simulation, inference and model reduction may be systematically derived. The useful consequences are potentially far-reaching in computational science, machine learning and beyond. Hybrid compositional stochastic modeling/probabilistic programming approaches may also be possible.

Stochastic Process Semantics for Dynamical Grammar Syntax: An Overview

We define a class of probabilistic models in terms of an operator algebra of stochastic processes, and a representation for this class in terms of stochastic parameterized grammars. A syntactic specification of a grammar is mapped to semantics given in terms of a ring of operators, so that grammatical composition corresponds to operator addition or multiplication. The operators are generators for the time-evolution of stochastic processes. Within this modeling framework one can express data clustering models, logic programs, ordinary and stochastic differential equations, graph grammars, and stochastic chemical reaction kinetics. This mathematical formulation connects these apparently distant fields to one another and to mathematical methods from quantum field theory and operator algebra.