Lithium-Ion Battery System Health Monitoring and Fault Analysis from Field Data Using Gaussian Processes

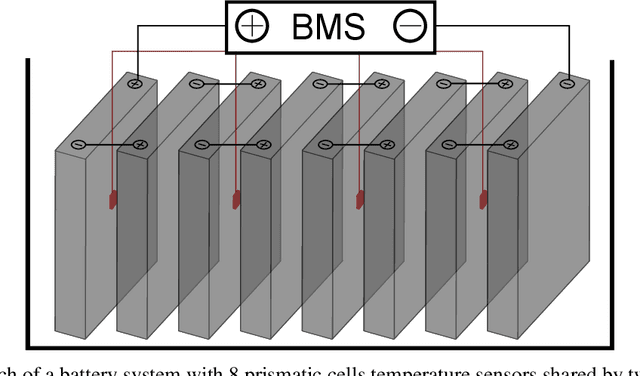
Health monitoring, fault analysis, and detection are critical for the safe and sustainable operation of battery systems. We apply Gaussian process resistance models on lithium iron phosphate battery field data to effectively separate the time-dependent and operating point-dependent resistance. The data set contains 29 battery systems returned to the manufacturer for warranty, each with eight cells in series, totaling 232 cells and 131 million data rows. We develop probabilistic fault detection rules using recursive spatiotemporal Gaussian processes. These processes allow the quick processing of over a million data points, enabling advanced online monitoring and furthering the understanding of battery pack failure in the field. The analysis underlines that often, only a single cell shows abnormal behavior or a knee point, consistent with weakest-link failure for cells connected in series, amplified by local resistive heating. The results further the understanding of how batteries degrade and fail in the field and demonstrate the potential of efficient online monitoring based on data. We open-source the code and publish the large data set upon completion of the review of this article.

Interpretation of High-Dimensional Linear Regression: Effects of Nullspace and Regularization Demonstrated on Battery Data

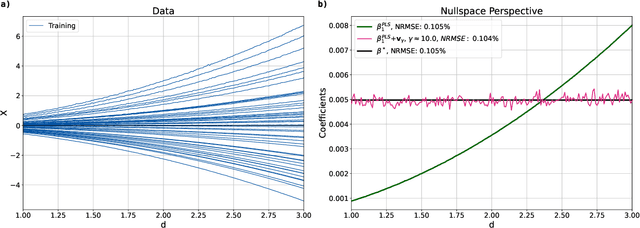
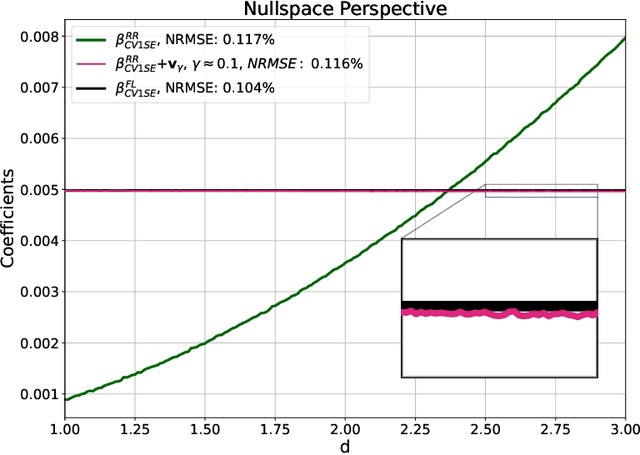
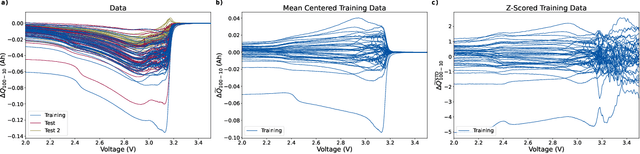
High-dimensional linear regression is important in many scientific fields. This article considers discrete measured data of underlying smooth latent processes, as is often obtained from chemical or biological systems. Interpretation in high dimensions is challenging because the nullspace and its interplay with regularization shapes regression coefficients. The data's nullspace contains all coefficients that satisfy $\mathbf{Xw}=\mathbf{0}$, thus allowing very different coefficients to yield identical predictions. We developed an optimization formulation to compare regression coefficients and coefficients obtained by physical engineering knowledge to understand which part of the coefficient differences are close to the nullspace. This nullspace method is tested on a synthetic example and lithium-ion battery data. The case studies show that regularization and z-scoring are design choices that, if chosen corresponding to prior physical knowledge, lead to interpretable regression results. Otherwise, the combination of the nullspace and regularization hinders interpretability and can make it impossible to obtain regression coefficients close to the true coefficients when there is a true underlying linear model. Furthermore, we demonstrate that regression methods that do not produce coefficients orthogonal to the nullspace, such as fused lasso, can improve interpretability. In conclusion, the insights gained from the nullspace perspective help to make informed design choices for building regression models on high-dimensional data and reasoning about potential underlying linear models, which are important for system optimization and improving scientific understanding.