Modular Growth of Hierarchical Networks: Efficient, General, and Robust Curriculum Learning

Structural modularity is a pervasive feature of biological neural networks, which have been linked to several functional and computational advantages. Yet, the use of modular architectures in artificial neural networks has been relatively limited despite early successes. Here, we explore the performance and functional dynamics of a modular network trained on a memory task via an iterative growth curriculum. We find that for a given classical, non-modular recurrent neural network (RNN), an equivalent modular network will perform better across multiple metrics, including training time, generalizability, and robustness to some perturbations. We further examine how different aspects of a modular network's connectivity contribute to its computational capability. We then demonstrate that the inductive bias introduced by the modular topology is strong enough for the network to perform well even when the connectivity within modules is fixed and only the connections between modules are trained. Our findings suggest that gradual modular growth of RNNs could provide advantages for learning increasingly complex tasks on evolutionary timescales, and help build more scalable and compressible artificial networks.

Network bottlenecks and task structure control the evolution of interpretable learning rules in a foraging agent

Developing reliable mechanisms for continuous local learning is a central challenge faced by biological and artificial systems. Yet, how the environmental factors and structural constraints on the learning network influence the optimal plasticity mechanisms remains obscure even for simple settings. To elucidate these dependencies, we study meta-learning via evolutionary optimization of simple reward-modulated plasticity rules in embodied agents solving a foraging task. We show that unconstrained meta-learning leads to the emergence of diverse plasticity rules. However, regularization and bottlenecks to the model help reduce this variability, resulting in interpretable rules. Our findings indicate that the meta-learning of plasticity rules is very sensitive to various parameters, with this sensitivity possibly reflected in the learning rules found in biological networks. When included in models, these dependencies can be used to discover potential objective functions and details of biological learning via comparisons with experimental observations.

Emergent mechanisms for long timescales depend on training curriculum and affect performance in memory tasks

Recurrent neural networks (RNNs) in the brain and in silico excel at solving tasks with intricate temporal dependencies. Long timescales required for solving such tasks can arise from properties of individual neurons (single-neuron timescale, $\tau$, e.g., membrane time constant in biological neurons) or recurrent interactions among them (network-mediated timescale). However, the contribution of each mechanism for optimally solving memory-dependent tasks remains poorly understood. Here, we train RNNs to solve $N$-parity and $N$-delayed match-to-sample tasks with increasing memory requirements controlled by $N$ by simultaneously optimizing recurrent weights and $\tau$s. We find that for both tasks RNNs develop longer timescales with increasing $N$, but depending on the learning objective, they use different mechanisms. Two distinct curricula define learning objectives: sequential learning of a single-$N$ (single-head) or simultaneous learning of multiple $N$s (multi-head). Single-head networks increase their $\tau$ with $N$ and are able to solve tasks for large $N$, but they suffer from catastrophic forgetting. However, multi-head networks, which are explicitly required to hold multiple concurrent memories, keep $\tau$ constant and develop longer timescales through recurrent connectivity. Moreover, we show that the multi-head curriculum increases training speed and network stability to ablations and perturbations, and allows RNNs to generalize better to tasks beyond their training regime. This curriculum also significantly improves training GRUs and LSTMs for large-$N$ tasks. Our results suggest that adapting timescales to task requirements via recurrent interactions allows learning more complex objectives and improves the RNN's performance.

Locally adaptive cellular automata for goal-oriented self-organization

The essential ingredient for studying the phenomena of emergence is the ability to generate and manipulate emergent systems that span large scales. Cellular automata are the model class particularly known for their effective scalability but are also typically constrained by fixed local rules. In this paper, we propose a new model class of adaptive cellular automata that allows for the generation of scalable and expressive models. We show how to implement computation-effective adaptation by coupling the update rule of the cellular automaton with itself and the system state in a localized way. To demonstrate the applications of this approach, we implement two different emergent models: a self-organizing Ising model and two types of plastic neural networks, a rate and spiking model. With the Ising model, we show how coupling local/global temperatures to local/global measurements can tune the model to stay in the vicinity of the critical temperature. With the neural models, we reproduce a classical balanced state in large recurrent neuronal networks with excitatory and inhibitory neurons and various plasticity mechanisms. Our study opens multiple directions for studying collective behavior and emergence.

The dynamical regime and its importance for evolvability, task performance and generalization

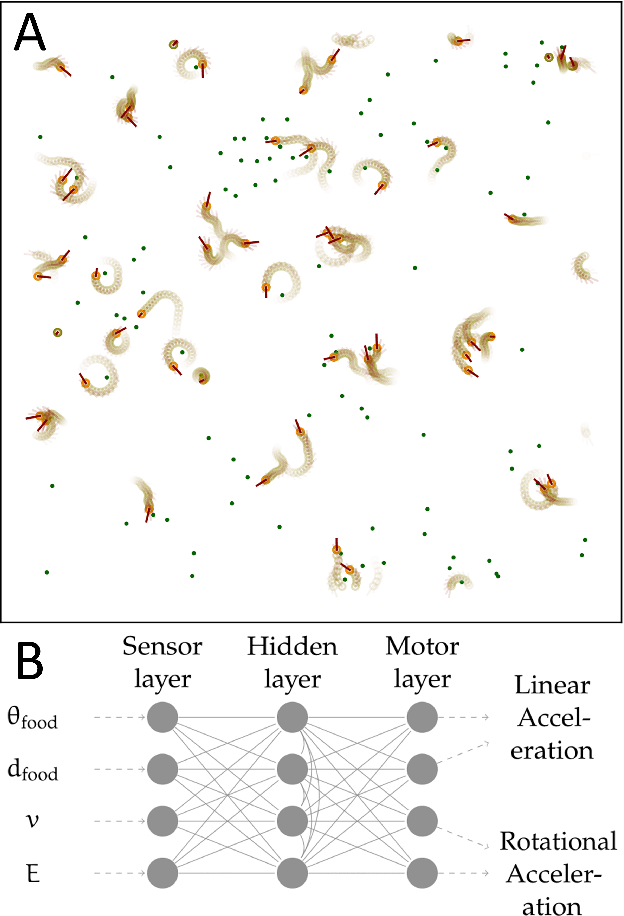
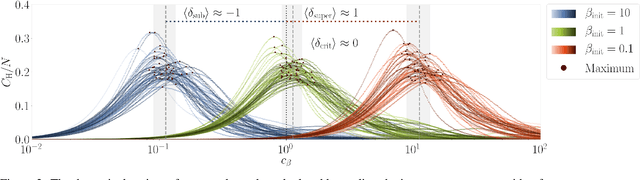
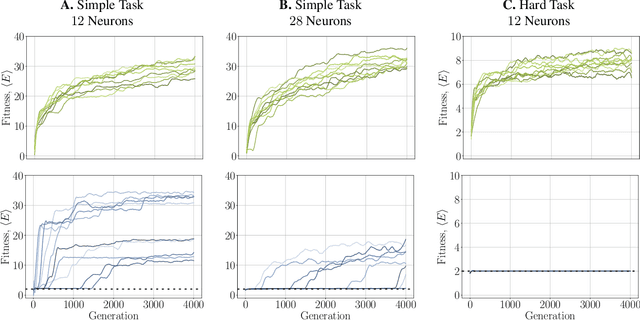
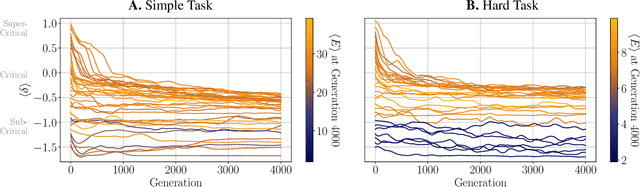
It has long been hypothesized that operating close to the critical state is beneficial for natural and artificial systems. We test this hypothesis by evolving foraging agents controlled by neural networks that can change the system's dynamical regime throughout evolution. Surprisingly, we find that all populations, regardless of their initial regime, evolve to be subcritical in simple tasks and even strongly subcritical populations can reach comparable performance. We hypothesize that the moderately subcritical regime combines the benefits of generalizability and adaptability brought by closeness to criticality with the stability of the dynamics characteristic for subcritical systems. By a resilience analysis, we find that initially critical agents maintain their fitness level even under environmental changes and degrade slowly with increasing perturbation strength. On the other hand, subcritical agents originally evolved to the same fitness, were often rendered utterly inadequate and degraded faster. We conclude that although the subcritical regime is preferable for a simple task, the optimal deviation from criticality depends on the task difficulty: for harder tasks, agents evolve closer to criticality. Furthermore, subcritical populations cannot find the path to decrease their distance to criticality. In summary, our study suggests that initializing models near criticality is important to find an optimal and flexible solution.