Benchmarking Large Language Models for Math Reasoning Tasks

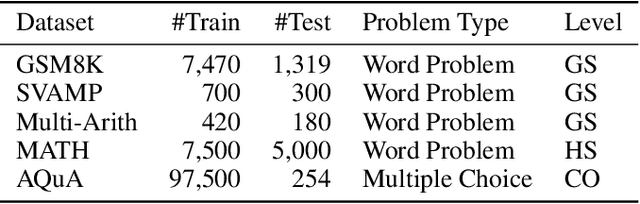
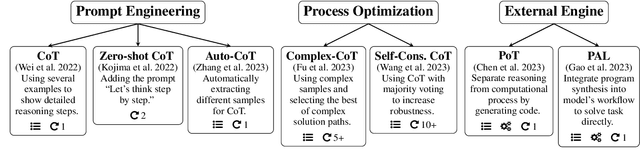
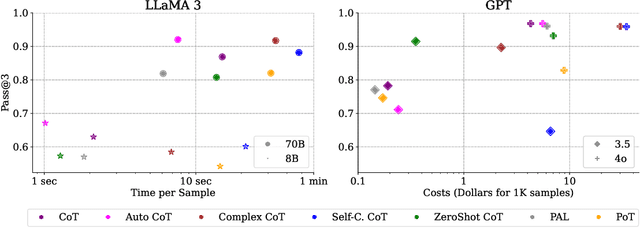
The use of Large Language Models (LLMs) in mathematical reasoning has become a cornerstone of related research, demonstrating the intelligence of these models and enabling potential practical applications through their advanced performance, such as in educational settings. Despite the variety of datasets and in-context learning algorithms designed to improve the ability of LLMs to automate mathematical problem solving, the lack of comprehensive benchmarking across different datasets makes it complicated to select an appropriate model for specific tasks. In this project, we present a benchmark that fairly compares seven state-of-the-art in-context learning algorithms for mathematical problem solving across five widely used mathematical datasets on four powerful foundation models. Furthermore, we explore the trade-off between efficiency and performance, highlighting the practical applications of LLMs for mathematical reasoning. Our results indicate that larger foundation models like GPT-4o and LLaMA 3-70B can solve mathematical reasoning independently from the concrete prompting strategy, while for smaller models the in-context learning approach significantly influences the performance. Moreover, the optimal prompt depends on the chosen foundation model. We open-source our benchmark code to support the integration of additional models in future research.

Stepwise Self-Consistent Mathematical Reasoning with Large Language Models

Using Large Language Models for complex mathematical reasoning is difficult, primarily due to the complexity of multi-step reasoning. The main challenges of this process include (1) selecting critical intermediate results to advance the procedure, and (2) limited exploration of potential solutions. To address these issues, we introduce a novel algorithm, namely Stepwise Self-Consistent Chain-of-Thought (SSC-CoT). SSC-CoT employs a strategy of selecting intermediate steps based on the intersection of various reasoning chains. Additionally, SSC-CoT enables the model to discover critical intermediate steps by querying a knowledge graph comprising relevant domain knowledge. To validate SSC-CoT, we present a new dataset, TriMaster100, tailored for complex trigonometry problems. This dataset contains 100 questions, with each solution broken down into scored intermediate steps, facilitating a comprehensive evaluation of the mathematical reasoning process. On TriMaster100, SSC-CoT triples the effectiveness of the state-of-the-art methods. Furthermore, we benchmark SSC-CoT on the widely recognized complex mathematical question dataset, MATH level 5, and it surpasses the second-best method by 7.2% in accuracy. Code and the TriMaster100 dataset can be found at: https://github.com/zhao-zilong/ssc-cot.