Automated discovery of finite volume schemes using Graph Neural Networks

Graph Neural Networks (GNNs) have deeply modified the landscape of numerical simulations by demonstrating strong capabilities in approximating solutions of physical systems. However, their ability to extrapolate beyond their training domain (\textit{e.g.} larger or structurally different graphs) remains uncertain. In this work, we establish that GNNs can serve purposes beyond their traditional role, and be exploited to generate numerical schemes, in conjunction with symbolic regression. First, we show numerically and theoretically that a GNN trained on a dataset consisting solely of two-node graphs can extrapolate a first-order Finite Volume (FV) scheme for the heat equation on out-of-distribution, unstructured meshes. Specifically, if a GNN achieves a loss $\varepsilon$ on such a dataset, it implements the FV scheme with an error of $\mathcal{O}(\varepsilon)$. Using symbolic regression, we show that the network effectively rediscovers the exact analytical formulation of the standard first-order FV scheme. We then extend this approach to an unsupervised context: the GNN recovers the first-order FV scheme using only a residual loss similar to Physics-Informed Neural Networks (PINNs) with no access to ground-truth data. Finally, we push the methodology further by considering higher-order schemes: we train (i) a 2-hop and (ii) a 2-layers GNN using the same PINN loss, that autonomously discover (i) a second-order correction term to the initial scheme using a 2-hop stencil, and (ii) the classic second-order midpoint scheme. These findings follows a recent paradigm in scientific computing: GNNs are not only strong approximators, but can be active contributors to the development of novel numerical methods.

Training Transformers for Mesh-Based Simulations

Simulating physics using Graph Neural Networks (GNNs) is predominantly driven by message-passing architectures, which face challenges in scaling and efficiency, particularly in handling large, complex meshes. These architectures have inspired numerous enhancements, including multigrid approaches and $K$-hop aggregation (using neighbours of distance $K$), yet they often introduce significant complexity and suffer from limited in-depth investigations. In response to these challenges, we propose a novel Graph Transformer architecture that leverages the adjacency matrix as an attention mask. The proposed approach incorporates innovative augmentations, including Dilated Sliding Windows and Global Attention, to extend receptive fields without sacrificing computational efficiency. Through extensive experimentation, we evaluate model size, adjacency matrix augmentations, positional encoding and $K$-hop configurations using challenging 3D computational fluid dynamics (CFD) datasets. We also train over 60 models to find a scaling law between training FLOPs and parameters. The introduced models demonstrate remarkable scalability, performing on meshes with up to 300k nodes and 3 million edges. Notably, the smallest model achieves parity with MeshGraphNet while being $7\times$ faster and $6\times$ smaller. The largest model surpasses the previous state-of-the-art by $38.8$\% on average and outperforms MeshGraphNet by $52$\% on the all-rollout RMSE, while having a similar training speed. Code and datasets are available at https://github.com/DonsetPG/graph-physics.

Dragonfly: a modular deep reinforcement learning library

Dragonfly is a deep reinforcement learning library focused on modularity, in order to ease experimentation and developments. It relies on a json serialization that allows to swap building blocks and perform parameter sweep, while minimizing code maintenance. Some of its features are specifically designed for CPU-intensive environments, such as numerical simulations. Its performance on standard agents using common benchmarks compares favorably with the literature.

MeshMask: Physics-Based Simulations with Masked Graph Neural Networks

We introduce a novel masked pre-training technique for graph neural networks (GNNs) applied to computational fluid dynamics (CFD) problems. By randomly masking up to 40\% of input mesh nodes during pre-training, we force the model to learn robust representations of complex fluid dynamics. We pair this masking strategy with an asymmetric encoder-decoder architecture and gated multi-layer perceptrons to further enhance performance. The proposed method achieves state-of-the-art results on seven CFD datasets, including a new challenging dataset of 3D intracranial aneurysm simulations with over 250,000 nodes per mesh. Moreover, it significantly improves model performance and training efficiency across such diverse range of fluid simulation tasks. We demonstrate improvements of up to 60\% in long-term prediction accuracy compared to previous best models, while maintaining similar computational costs. Notably, our approach enables effective pre-training on multiple datasets simultaneously, significantly reducing the time and data required to achieve high performance on new tasks. Through extensive ablation studies, we provide insights into the optimal masking ratio, architectural choices, and training strategies.

Multi-Grid Graph Neural Networks with Self-Attention for Computational Mechanics

Advancement in finite element methods have become essential in various disciplines, and in particular for Computational Fluid Dynamics (CFD), driving research efforts for improved precision and efficiency. While Convolutional Neural Networks (CNNs) have found success in CFD by mapping meshes into images, recent attention has turned to leveraging Graph Neural Networks (GNNs) for direct mesh processing. This paper introduces a novel model merging Self-Attention with Message Passing in GNNs, achieving a 15\% reduction in RMSE on the well known flow past a cylinder benchmark. Furthermore, a dynamic mesh pruning technique based on Self-Attention is proposed, that leads to a robust GNN-based multigrid approach, also reducing RMSE by 15\%. Additionally, a new self-supervised training method based on BERT is presented, resulting in a 25\% RMSE reduction. The paper includes an ablation study and outperforms state-of-the-art models on several challenging datasets, promising advancements similar to those recently achieved in natural language and image processing. Finally, the paper introduces a dataset with meshes larger than existing ones by at least an order of magnitude. Code and Datasets will be released at https://github.com/DonsetPG/multigrid-gnn.

Beacon, a lightweight deep reinforcement learning benchmark library for flow control

Recently, the increasing use of deep reinforcement learning for flow control problems has led to a new area of research, focused on the coupling and the adaptation of the existing algorithms to the control of numerical fluid dynamics environments. Although still in its infancy, the field has seen multiple successes in a short time span, and its fast development pace can certainly be partly imparted to the open-source effort that drives the expansion of the community. Yet, this emerging domain still misses a common ground to (i) ensure the reproducibility of the results, and (ii) offer a proper ad-hoc benchmarking basis. To this end, we propose Beacon, an open-source benchmark library composed of seven lightweight 1D and 2D flow control problems with various characteristics, action and observation space characteristics, and CPU requirements. In this contribution, the seven considered problems are described, and reference control solutions are provided. The sources for the following work are available at https://github.com/jviquerat/beacon.

Robust deep learning for emulating turbulent viscosities

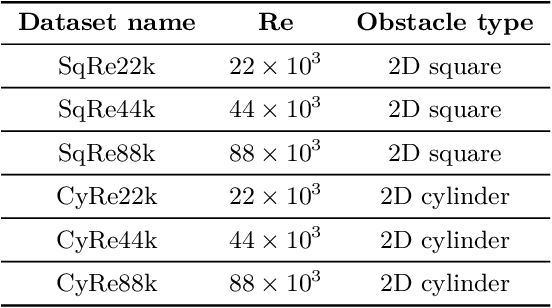
From the simplest models to complex deep neural networks, modeling turbulence with machine learning techniques still offers multiple challenges. In this context, the present contribution proposes a robust strategy using patch-based training to learn turbulent viscosity from flow velocities, and demonstrates its efficient use on the Spallart-Allmaras turbulence model. Training datasets are generated for flow past two-dimensional (2D) obstacles at high Reynolds numbers and used to train an auto-encoder type convolutional neural network with local patch inputs. Compared to a standard training technique, patch-based learning not only yields increased accuracy but also reduces the computational cost required for training.

A review on Deep Reinforcement Learning for Fluid Mechanics

Deep reinforcement learning (DRL) has recently been adopted in a wide range of physics and engineering domains for its ability to solve decision-making problems that were previously out of reach due to a combination of non-linearity and high dimensionality. In the last few years, it has spread in the field of computational mechanics, and particularly in fluid dynamics, with recent applications in flow control and shape optimization. In this work, we conduct a detailed review of existing DRL applications to fluid mechanics problems. In addition, we present recent results that further illustrate the potential of DRL in Fluid Mechanics. The coupling methods used in each case are covered, detailing their advantages and limitations. Our review also focuses on the comparison with classical methods for optimal control and optimization. Finally, several test cases are described that illustrate recent progress made in this field. The goal of this publication is to provide an understanding of DRL capabilities along with state-of-the-art applications in fluid dynamics to researchers wishing to address new problems with these methods.