QoS-Nets: Adaptive Approximate Neural Network Inference

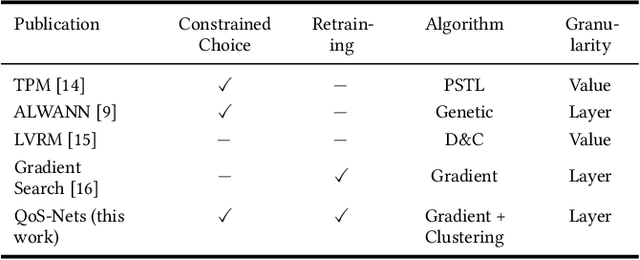
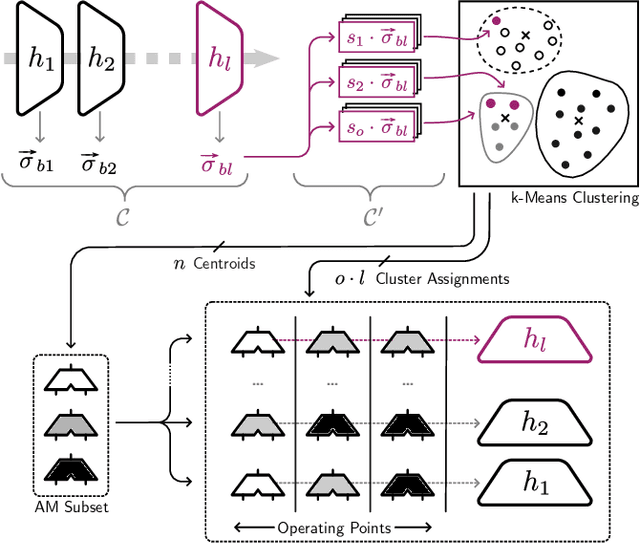
In order to vary the arithmetic resource consumption of neural network applications at runtime, this work proposes the flexible reuse of approximate multipliers for neural network layer computations. We introduce a search algorithm that chooses an appropriate subset of approximate multipliers of a user-defined size from a larger search space and enables retraining to maximize task performance. Unlike previous work, our approach can output more than a single, static assignment of approximate multiplier instances to layers. These different operating points allow a system to gradually adapt its Quality of Service (QoS) to changing environmental conditions by increasing or decreasing its accuracy and resource consumption. QoS-Nets achieves this by reassigning the selected approximate multiplier instances to layers at runtime. To combine multiple operating points with the use of retraining, we propose a fine-tuning scheme that shares the majority of parameters between operating points, with only a small amount of additional parameters required per operating point. In our evaluation on MobileNetV2, QoS-Nets is used to select four approximate multiplier instances for three different operating points. These operating points result in power savings for multiplications between 15.3% and 42.8% at a Top-5 accuracy loss between 0.3 and 2.33 percentage points. Through our fine-tuning scheme, all three operating points only increase the model's parameter count by only 2.75%.

Combining Gradients and Probabilities for Heterogeneous Approximation of Neural Networks

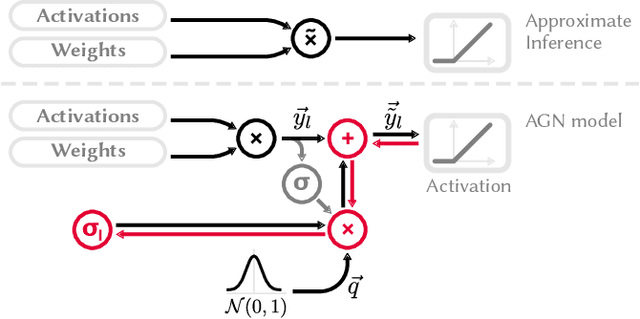
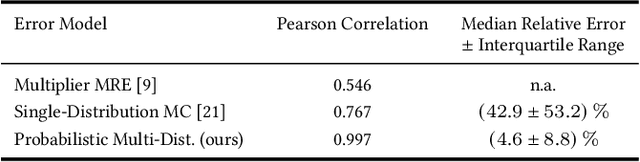
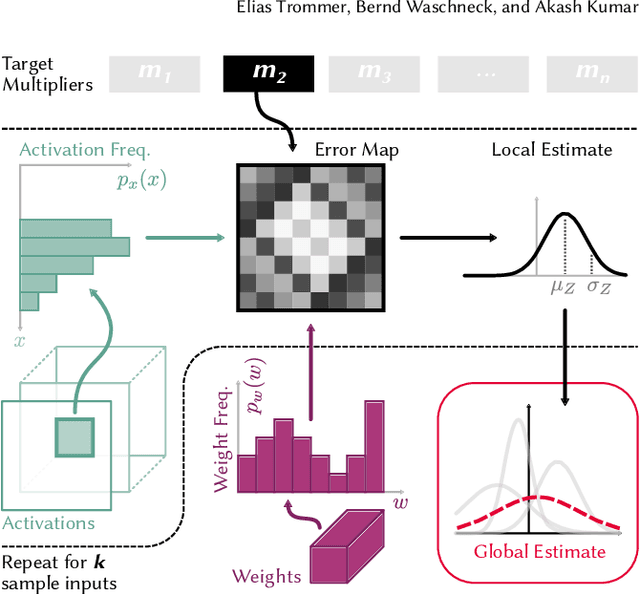
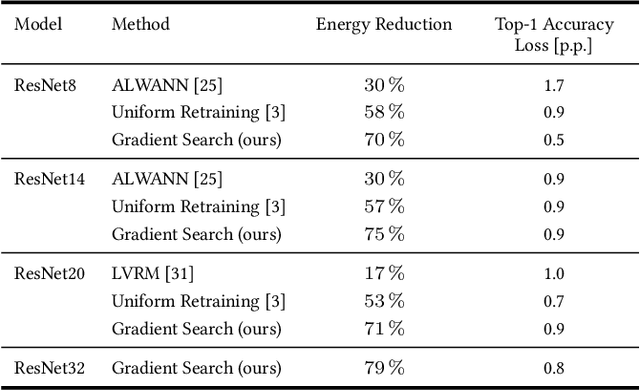
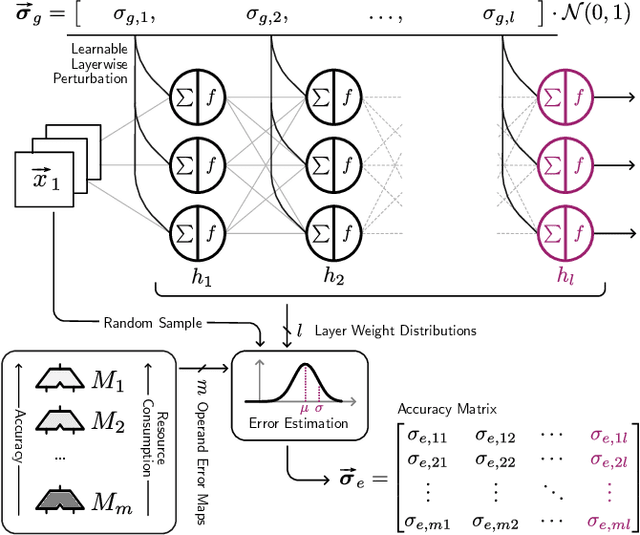
This work explores the search for heterogeneous approximate multiplier configurations for neural networks that produce high accuracy and low energy consumption. We discuss the validity of additive Gaussian noise added to accurate neural network computations as a surrogate model for behavioral simulation of approximate multipliers. The continuous and differentiable properties of the solution space spanned by the additive Gaussian noise model are used as a heuristic that generates meaningful estimates of layer robustness without the need for combinatorial optimization techniques. Instead, the amount of noise injected into the accurate computations is learned during network training using backpropagation. A probabilistic model of the multiplier error is presented to bridge the gap between the domains; the model estimates the standard deviation of the approximate multiplier error, connecting solutions in the additive Gaussian noise space to actual hardware instances. Our experiments show that the combination of heterogeneous approximation and neural network retraining reduces the energy consumption for multiplications by 70% to 79% for different ResNet variants on the CIFAR-10 dataset with a Top-1 accuracy loss below one percentage point. For the more complex Tiny ImageNet task, our VGG16 model achieves a 53 % reduction in energy consumption with a drop in Top-5 accuracy of 0.5 percentage points. We further demonstrate that our error model can predict the parameters of an approximate multiplier in the context of the commonly used additive Gaussian noise (AGN) model with high accuracy. Our software implementation is available under https://github.com/etrommer/agn-approx.