Predicting center of mass position in non-cyclic activities: The influence of acceleration, prediction horizon, and ground reaction forces

The whole-body center of mass (CoM) plays an important role in quantifying human movement. Prediction of future CoM trajectory, modeled as a point mass under influence of external forces, can be a surrogate for inferring intent. Given the current CoM position and velocity, predicting the future CoM position by forward integration requires a forecast of CoM accelerations during the prediction horizon. However, it is unclear how assumptions about the acceleration, prediction horizon length, and information from ground reaction forces (GRFs), which provide the instantaneous acceleration, affect the prediction. We study these factors by analyzing data of 10 healthy young adults performing 14 non-cyclic activities. We assume that the acceleration during a horizon will be 1) zero, 2) remain constant, or 3) converge to zero as a cubic trajectory, and perform predictions for horizons of 125 to 625 milliseconds. We quantify the prediction performance by comparing the position error and accuracy of identifying the main direction of displacement against trajectories obtained from a whole-body marker set. For all the assumed accelerations profiles, position errors grow quadratically with horizon length ($R^2 > 0.930$) while the accuracy of the predicted direction decreases linearly ($R^2>0.615$). Post-hoc tests reveal that the constant and cubic profiles, which utilize the GRFs, outperform the zero-acceleration assumption in position error ($p<0.001$, Cohen's $d>3.23$) and accuracy ($p<0.034$, Cohen's $d>1.44)$ at horizons of 125 and 250$\,ms$. The results provide evidence for benefits of incorporating GRFs into predictions and point to 250$\,ms$ as a threshold for horizon length in predictive applications.

Extending the Benefits of Parallel Elasticity across Multiple Actuation Tasks: A Geometric and Optimization-Based Approach

A spring in parallel with an effort source (e.g., electric motor or human muscle) can reduce its energy consumption and effort (i.e., torque or force) depending on the spring stiffness, spring preload, and actuation task. However, selecting the spring stiffness and preload that guarantees effort or energy reduction for an arbitrary set of tasks is a design challenge. This work formulates a convex optimization problem to guarantee that a parallel spring reduces the root-mean-square source effort or energy consumption for multiple tasks. Specifically, we guarantee the benefits across multiple tasks by enforcing a set of convex quadratic constraints in our optimization variables -- the parallel spring stiffness and preload. These quadratic constraints are equivalent to ellipses in the stiffness and preload plane, any combination of stiffness and preload inside the ellipse represents a parallel spring that minimizes effort source or energy consumption with respect to an actuator without a spring. This geometric interpretation intuitively guides the stiffness and preload selection process. We analytically and experimentally prove the convex quadratic function of the spring stiffness and preload. As applications, we analyze the stiffness and preload selection of a parallel spring for a knee exoskeleton using human muscle as the effort source and a prosthetic ankle powered by electric motors. To promote adoption, the optimization and geometric methods are available as supplemental open-source software that can be executed in a web browser.

Lower-limb kinematics and kinetics during continuously varying human locomotion

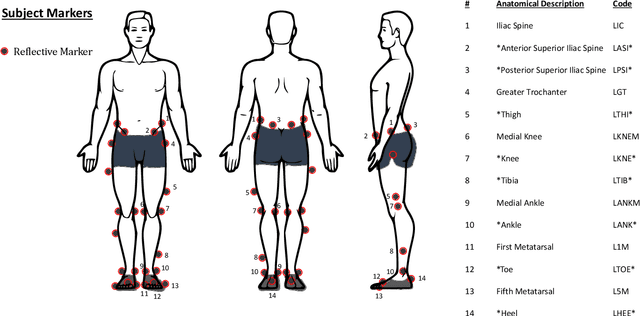
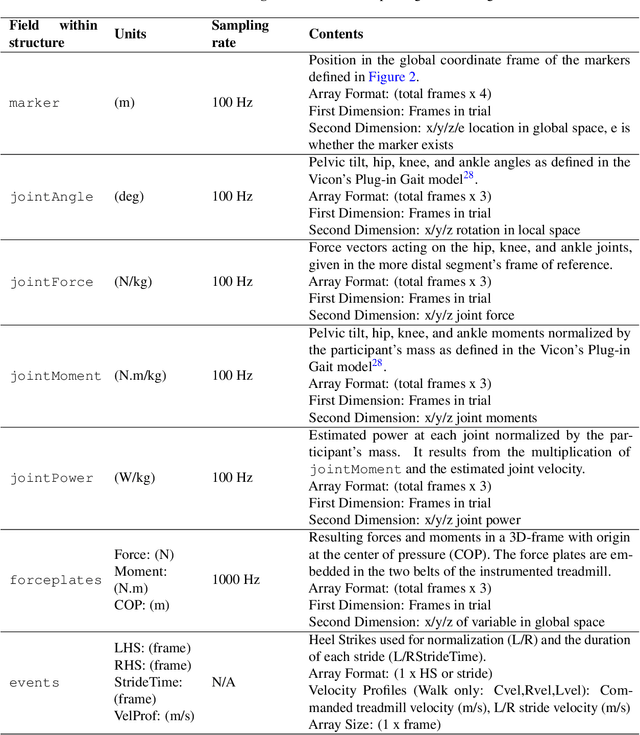
Human locomotion involves continuously variable activities including walking, running, and stair climbing over a range of speeds and inclinations as well as sit-stand, walk-run, and walk-stairs transitions. Understanding the kinematics and kinetics of the lower limbs during continuously varying locomotion is fundamental to developing robotic prostheses and exoskeletons that assist in community ambulation. However, available datasets on human locomotion neglect transitions between activities and/or continuous variations in speed and inclination during these activities. This data paper reports a new dataset that includes the lower-limb kinematics and kinetics of ten able-bodied participants walking at multiple inclines ($\pm$ 0, 5, 10 $^{\circ}$) and speeds (0.8, 1, 1.2 m/s), running at multiple speeds (1.8, 2, 2.2, 2.4 m/s), walking and running with constant acceleration ($\pm$ 0.2, 0.5 $\text{m/s^2}$), and stair ascent/descent with multiple stair inclines (20, 25, 30, 35 $^{\circ}$). This dataset also includes sit-stand transitions, walk-run transitions, and walk-stairs transitions. Data were recorded by a Vicon motion capture system and, for applicable tasks, a Bertec instrumented treadmill.