What is the relationship between Slow Feature Analysis and the Successor Representation?

(This is a work in progress. Feedback is welcome) An analytical comparison is made between slow feature analysis (SFA) and the successor representation (SR). While SFA and the SR stem from distinct areas of machine learning, they share important properties, both in terms of their mathematics and the types of information they are sensitive to. This work studies their connection along these two axes. In particular, multiple variants of the SFA algorithm are explored analytically and then applied to the setting of an MDP, leading to a family of eigenvalue problems involving the SR and other related quantities. These resulting eigenvalue problems are then illustrated in the toy setting of a gridworld, where it is demonstrated that the place- and grid-like fields often associated to the SR can equally be generated using SFA.

A Tutorial on the Spectral Theory of Markov Chains

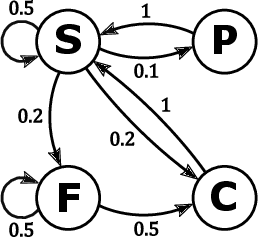
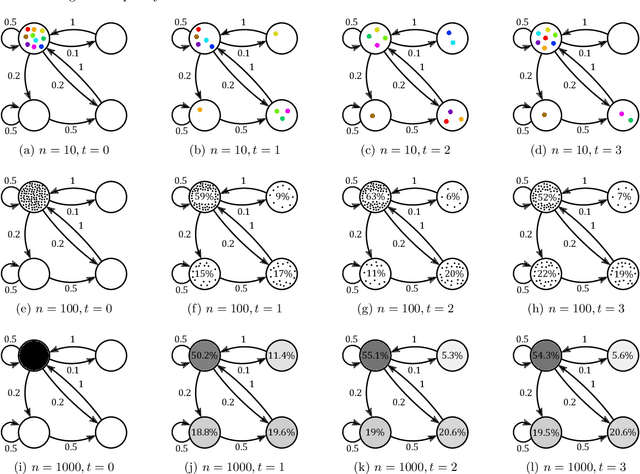
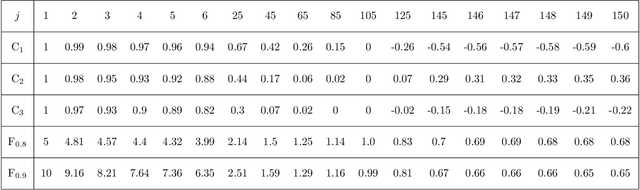
Markov chains are a class of probabilistic models that have achieved widespread application in the quantitative sciences. This is in part due to their versatility, but is compounded by the ease with which they can be probed analytically. This tutorial provides an in-depth introduction to Markov chains, and explores their connection to graphs and random walks. We utilize tools from linear algebra and graph theory to describe the transition matrices of different types of Markov chains, with a particular focus on exploring properties of the eigenvalues and eigenvectors corresponding to these matrices. The results presented are relevant to a number of methods in machine learning and data mining, which we describe at various stages. Rather than being a novel academic study in its own right, this text presents a collection of known results, together with some new concepts. Moreover, the tutorial focuses on offering intuition to readers rather than formal understanding, and only assumes basic exposure to concepts from linear algebra and probability theory. It is therefore accessible to students and researchers from a wide variety of disciplines.