What is the relationship between Slow Feature Analysis and the Successor Representation?
Paper and Code
Sep 25, 2024


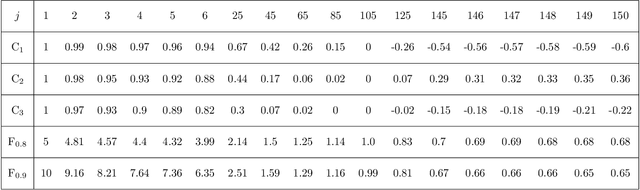
(This is a work in progress. Feedback is welcome) An analytical comparison is made between slow feature analysis (SFA) and the successor representation (SR). While SFA and the SR stem from distinct areas of machine learning, they share important properties, both in terms of their mathematics and the types of information they are sensitive to. This work studies their connection along these two axes. In particular, multiple variants of the SFA algorithm are explored analytically and then applied to the setting of an MDP, leading to a family of eigenvalue problems involving the SR and other related quantities. These resulting eigenvalue problems are then illustrated in the toy setting of a gridworld, where it is demonstrated that the place- and grid-like fields often associated to the SR can equally be generated using SFA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge