Bias-Corrected Peaks-Over-Threshold Estimation of the CVaR

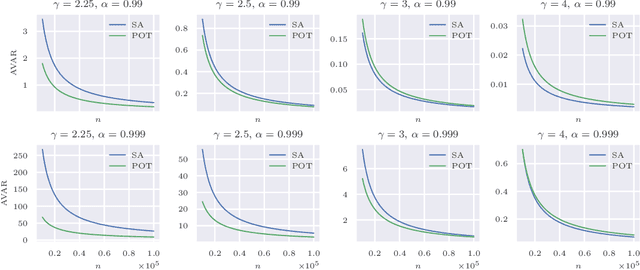
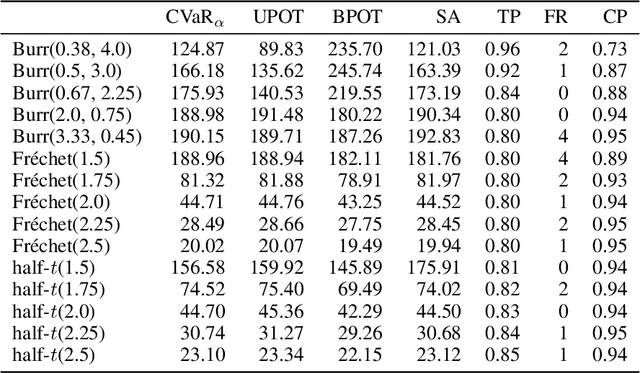
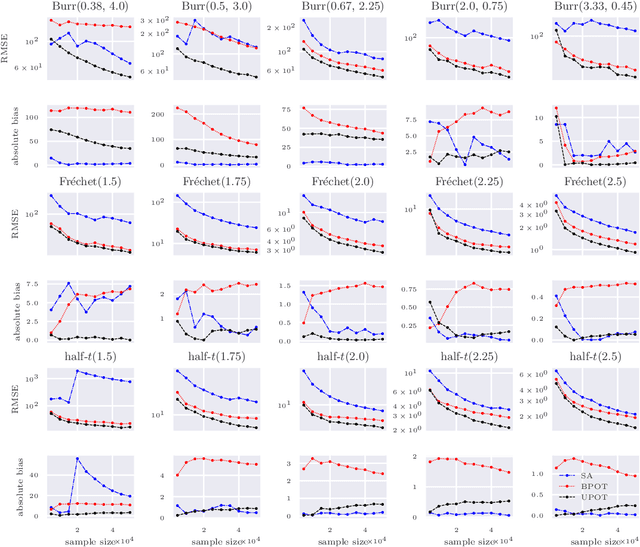
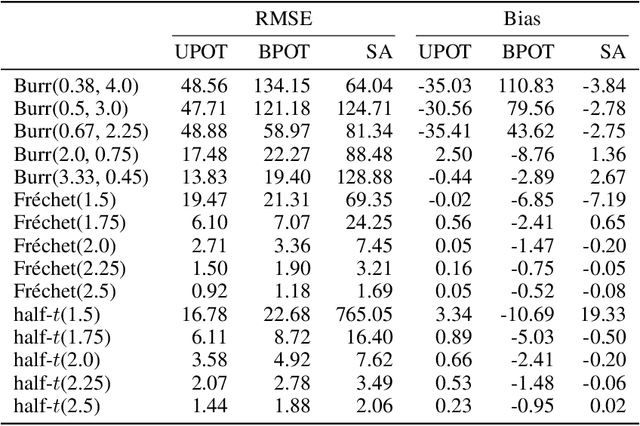
The conditional value-at-risk (CVaR) is a useful risk measure in fields such as machine learning, finance, insurance, energy, etc. When measuring very extreme risk, the commonly used CVaR estimation method of sample averaging does not work well due to limited data above the value-at-risk (VaR), the quantile corresponding to the CVaR level. To mitigate this problem, the CVaR can be estimated by extrapolating above a lower threshold than the VaR using a generalized Pareto distribution (GPD), which is often referred to as the peaks-over-threshold (POT) approach. This method often requires a very high threshold to fit well, leading to high variance in estimation, and can induce significant bias if the threshold is chosen too low. In this paper, we derive a new expression for the GPD approximation error of the CVaR, a bias term induced by the choice of threshold, as well as a bias correction method for the estimated GPD parameters. This leads to the derivation of a new estimator for the CVaR that we prove to be asymptotically unbiased. In a practical setting, we show through experiments that our estimator provides a significant performance improvement compared with competing CVaR estimators in finite samples. As a consequence of our bias correction method, it is also shown that a much lower threshold can be selected without introducing significant bias. This allows a larger portion of data to be be used in CVaR estimation compared with the typical POT approach, leading to more stable estimates. As secondary results, a new estimator for a second-order parameter of heavy-tailed distributions is derived, as well as a confidence interval for the CVaR which enables quantifying the level of variability in our estimator.

Risk-Averse Action Selection Using Extreme Value Theory Estimates of the CVaR

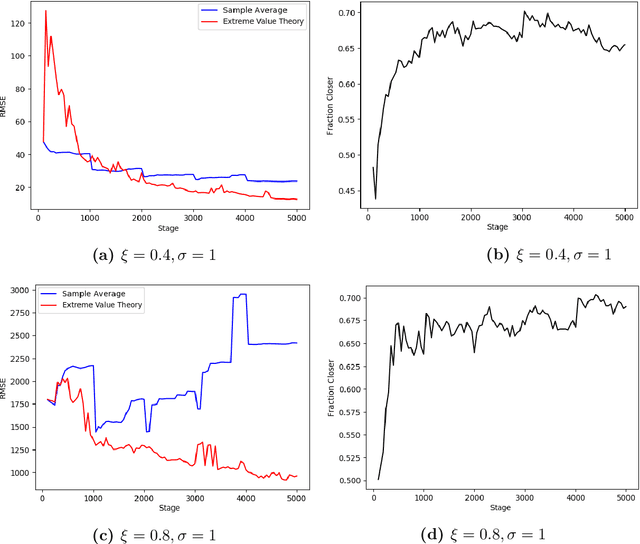
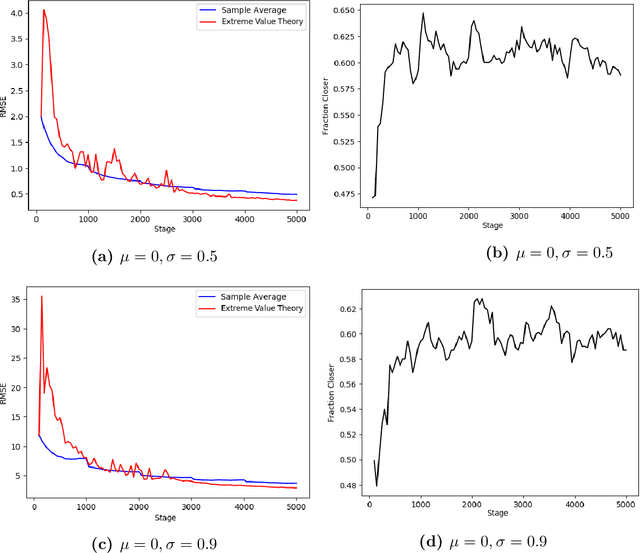
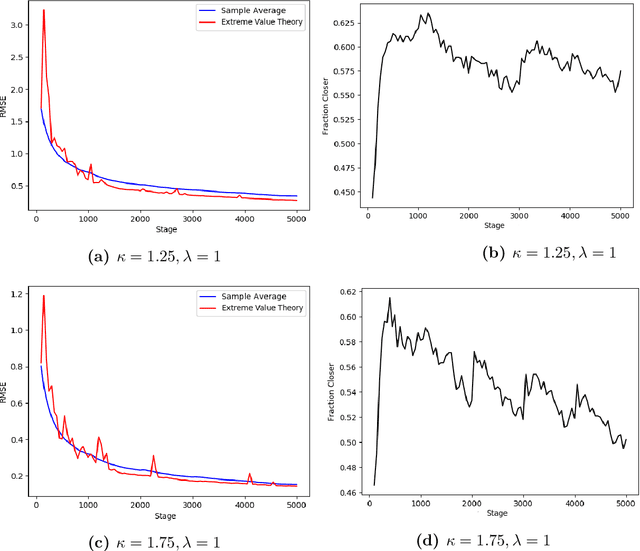
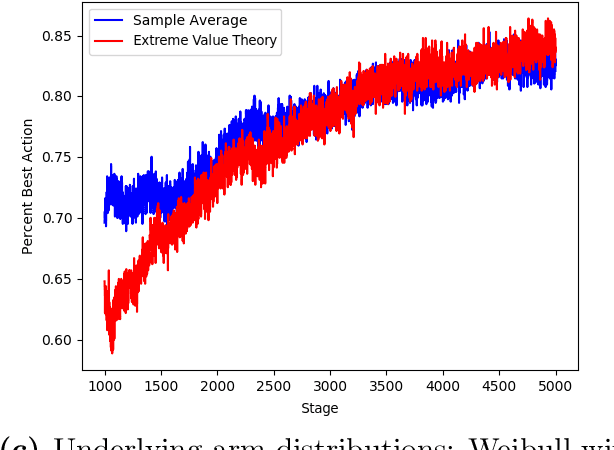
The Conditional Value-at-Risk (CVaR) is a useful risk measure in machine learning, finance, insurance, energy, etc. When the CVaR confidence parameter is very high, estimation by sample averaging exhibits high variance due to the limited number of samples above the corresponding threshold. To mitigate this problem, we present an estimation procedure for the CVaR that combines extreme value theory and a recently introduced method of automated threshold selection by Bader et al. (2018). Under appropriate conditions, we estimate the tail risk using a generalized Pareto distribution. We compare empirically this estimation procedure with the naive method of sample averaging, and show an improvement in accuracy for some specific cases. We also show how the estimation procedure can be used in reinforcement learning by applying our method to the multi-armed bandit problem where the goal is to avoid catastrophic risk.