Risk-Averse Action Selection Using Extreme Value Theory Estimates of the CVaR

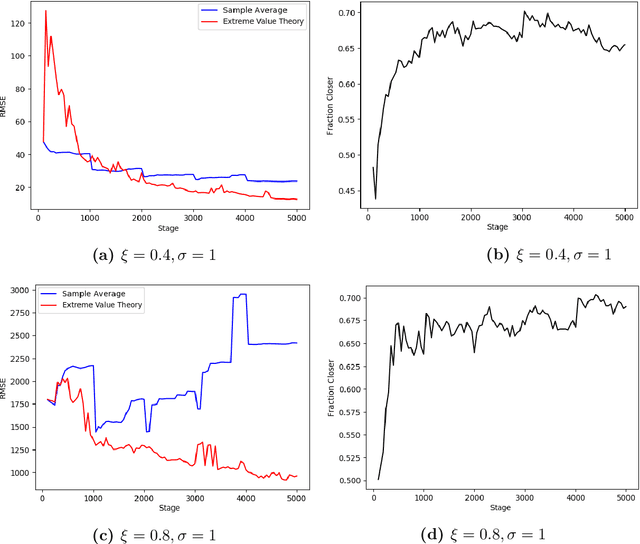
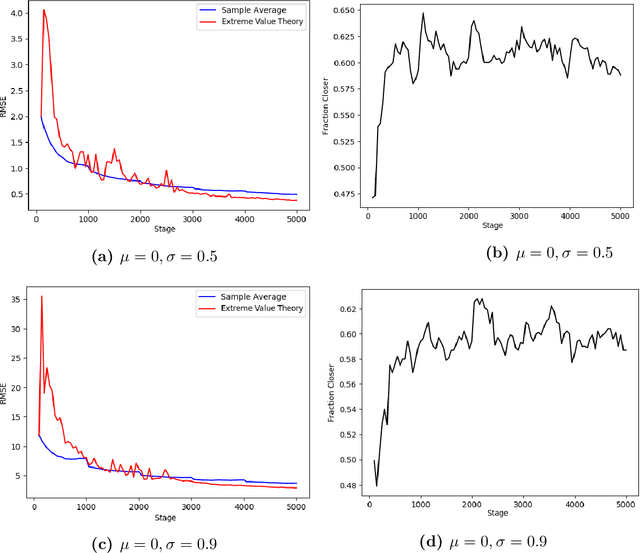
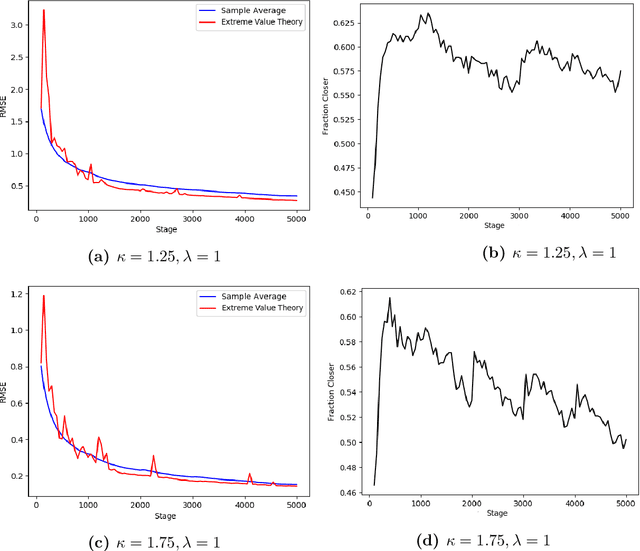
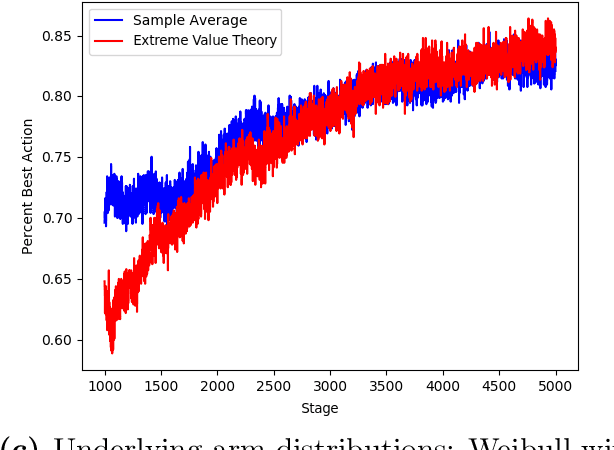
The Conditional Value-at-Risk (CVaR) is a useful risk measure in machine learning, finance, insurance, energy, etc. When the CVaR confidence parameter is very high, estimation by sample averaging exhibits high variance due to the limited number of samples above the corresponding threshold. To mitigate this problem, we present an estimation procedure for the CVaR that combines extreme value theory and a recently introduced method of automated threshold selection by Bader et al. (2018). Under appropriate conditions, we estimate the tail risk using a generalized Pareto distribution. We compare empirically this estimation procedure with the naive method of sample averaging, and show an improvement in accuracy for some specific cases. We also show how the estimation procedure can be used in reinforcement learning by applying our method to the multi-armed bandit problem where the goal is to avoid catastrophic risk.