QuATON: Quantization Aware Training of Optical Neurons

Optical neural architectures (ONAs) use coding elements with optimized physical parameters to perform intelligent measurements. However, fabricating ONAs while maintaining design performances is challenging. Limitations in fabrication techniques often limit the realizable precision of the trained parameters. Physical constraints may also limit the range of values the physical parameters can hold. Thus, ONAs should be trained within the implementable constraints. However, such physics-based constraints reduce the training objective to a constrained optimization problem, making it harder to optimize with existing gradient-based methods. To alleviate these critical issues that degrade performance from simulation to realization we propose a physics-informed quantization-aware training framework. Our approach accounts for the physical constraints during the training process, leading to robust designs. We evaluate our approach on an ONA proposed in the literature, named a diffractive deep neural network (D2NN), for all-optical phase imaging and for classification of phase objects. With extensive experiments on different quantization levels and datasets, we show that our approach leads to ONA designs that are robust to quantization noise.

Differentiable Microscopy Designs an All Optical Quantitative Phase Microscope

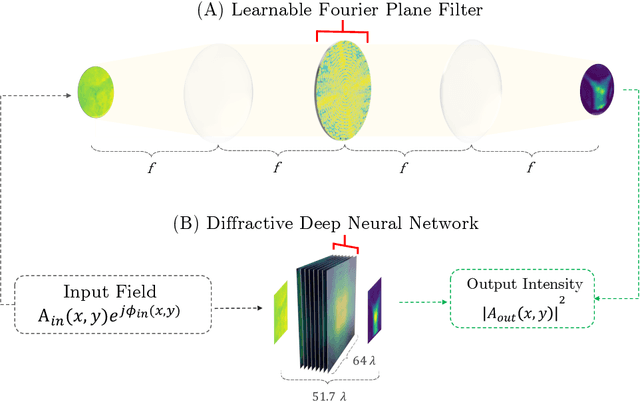
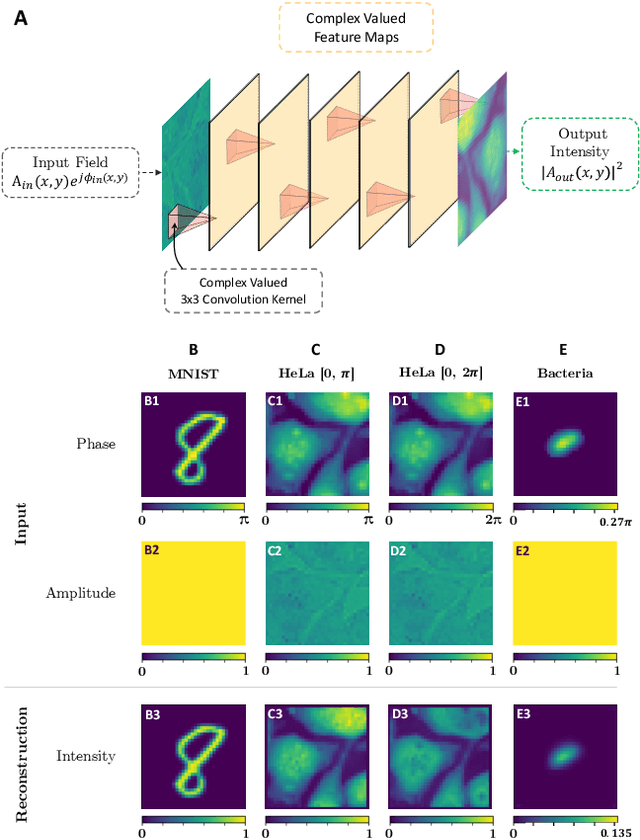
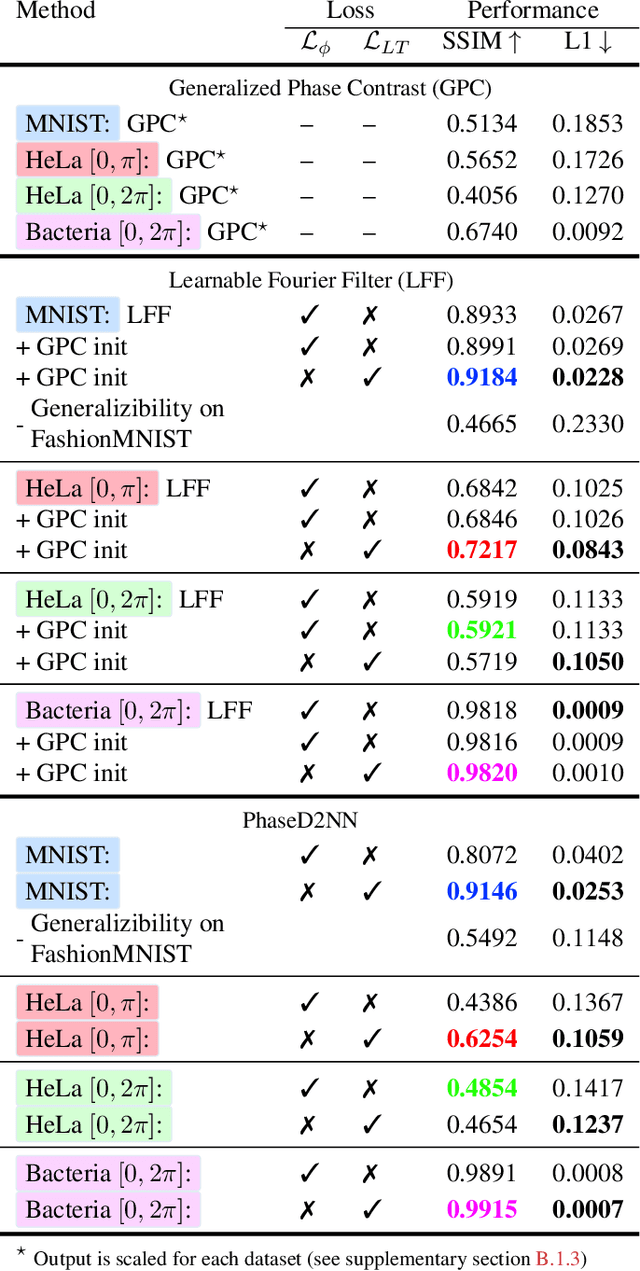
Ever since the first microscope by Zacharias Janssen in the late 16th century, scientists have been inventing new types of microscopes for various tasks. Inventing a novel architecture demands years, if not decades, worth of scientific experience and creativity. In this work, we introduce Differentiable Microscopy ($\partial\mu$), a deep learning-based design paradigm, to aid scientists design new interpretable microscope architectures. Differentiable microscopy first models a common physics-based optical system however with trainable optical elements at key locations on the optical path. Using pre-acquired data, we then train the model end-to-end for a task of interest. The learnt design proposal can then be simplified by interpreting the learnt optical elements. As a first demonstration, based on the optical 4-$f$ system, we present an all-optical quantitative phase microscope (QPM) design that requires no computational post-reconstruction. A follow-up literature survey suggested that the learnt architecture is similar to the generalized phase concept developed two decades ago. We then incorporate the generalized phase contrast concept to simplify the learning procedure. Furthermore, this physical optical setup is miniaturized using a diffractive deep neural network (D2NN). We outperform the existing benchmark for all-optical phase-to-intensity conversion on multiple datasets, and ours is the first demonstration of its kind on D2NNs. The proposed differentiable microscopy framework supplements the creative process of designing new optical systems and would perhaps lead to unconventional but better optical designs.

Differentiable Microscopy for Content and Task Aware Compressive Fluorescence Imaging

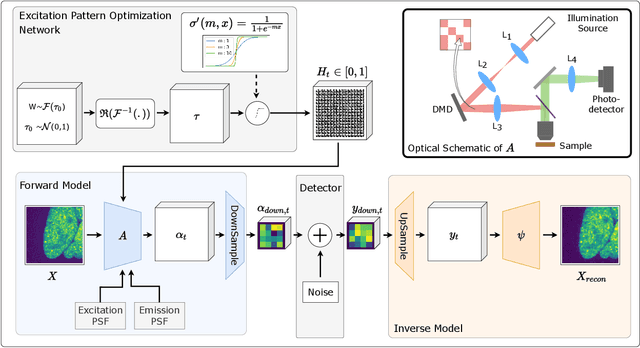
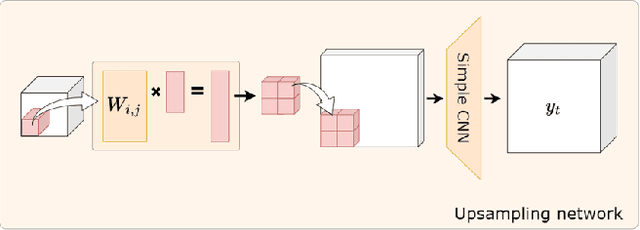
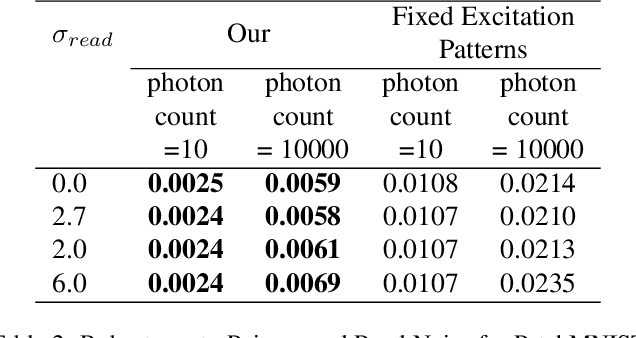
The trade-off between throughput and image quality is an inherent challenge in microscopy. To improve throughput, compressive imaging under-samples image signals; the images are then computationally reconstructed by solving a regularized inverse problem. Compared to traditional regularizers, Deep Learning based methods have achieved greater success in compression and image quality. However, the information loss in the acquisition process sets the compression bounds. Further improvement in compression, without compromising the reconstruction quality is thus a challenge. In this work, we propose differentiable compressive fluorescence microscopy ($\partial \mu$) which includes a realistic generalizable forward model with learnable-physical parameters (e.g. illumination patterns), and a novel physics-inspired inverse model. The cascaded model is end-to-end differentiable and can learn optimal compressive sampling schemes through training data. With our model, we performed thousands of numerical experiments on various compressive microscope configurations. Our results suggest that learned sampling outperforms widely used traditional compressive sampling schemes at higher compressions ($\times 100- 1000$) in terms of reconstruction quality. We further utilize our framework for Task Aware Compression. The experimental results show superior performance on segmentation tasks even at extremely high compression ($\times 4096$).