Dunge Liu
Multibeam Satellite Communications with Energy Efficiency Optimization
Mar 12, 2022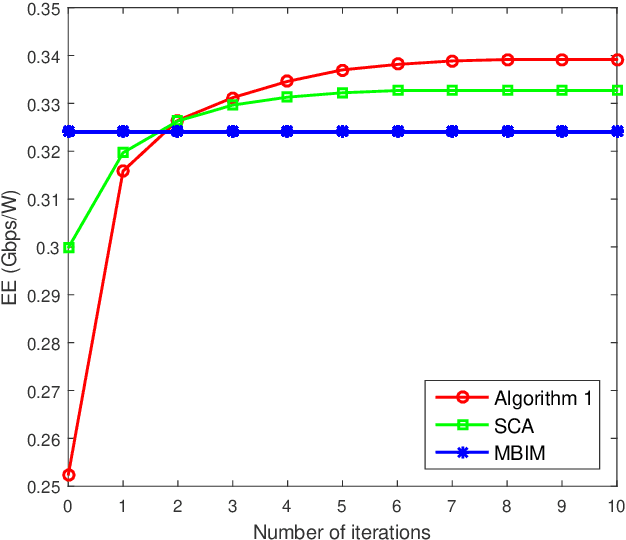
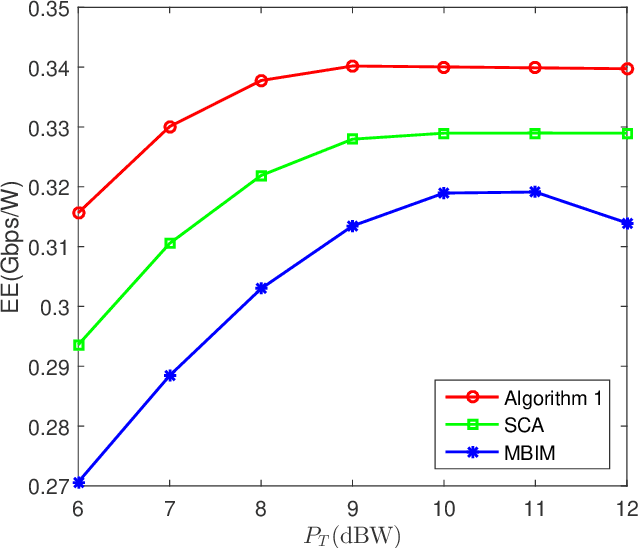
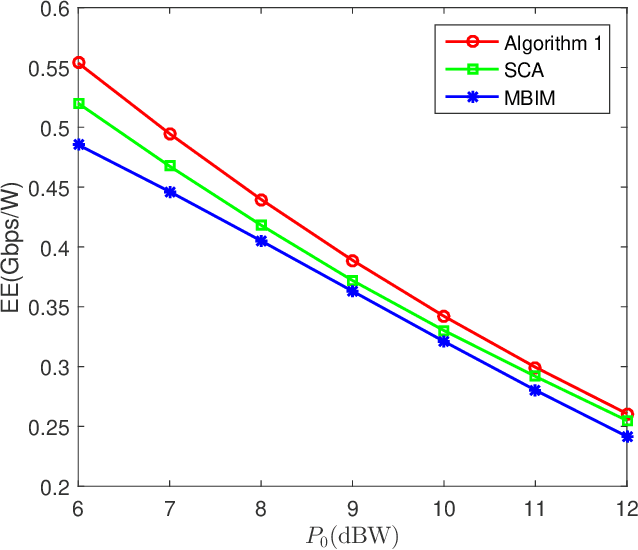

Abstract:Energy efficiency (EE) is an important aspect of satellite communications. Different with the existing algorithms that typically use the first-order Taylor lower bound approximation to convert non-convex EE maximization (EEM) problems into convex ones, in this letter a two-step quadratic transformation method is presented. In the first step, the fractional form of the achievable rate over the total power consumption is converted into a non-fractional form based on quadratic transformation. In the second step, the fractional form of the signal power over the interference-and-noise power is further converted into a non-fractional form, still based on quadratic transformation. After the two-step quadratic transformation, the original EEM problem is converted into an equivalent convex one. Then an alternating optimization algorithm is presented to solve it by iteratively performing two stages until a stop condition is satisfied. Simulation results show that the presented algorithm can fast converge and its performance is better than that of the sequential convex approximation algorithm and the multibeam interference mitigation algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge