On Probabilistic and Causal Reasoning with Summation Operators

Ibeling et al. (2023). axiomatize increasingly expressive languages of causation and probability, and Mosse et al. (2024) show that reasoning (specifically the satisfiability problem) in each causal language is as difficult, from a computational complexity perspective, as reasoning in its merely probabilistic or "correlational" counterpart. Introducing a summation operator to capture common devices that appear in applications -- such as the $do$-calculus of Pearl (2009) for causal inference, which makes ample use of marginalization -- van der Zander et al. (2023) partially extend these earlier complexity results to causal and probabilistic languages with marginalization. We complete this extension, fully characterizing the complexity of probabilistic and causal reasoning with summation, demonstrating that these again remain equally difficult. Surprisingly, allowing free variables for random variable values results in a system that is undecidable, so long as the ranges of these random variables are unrestricted. We finally axiomatize these languages featuring marginalization (or more generally summation), resolving open questions posed by Ibeling et al. (2023).

Comparing Causal Frameworks: Potential Outcomes, Structural Models, Graphs, and Abstractions

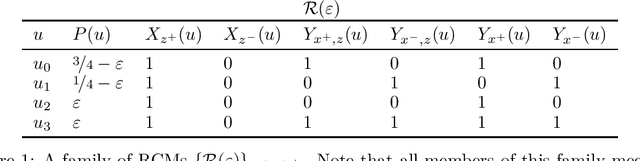
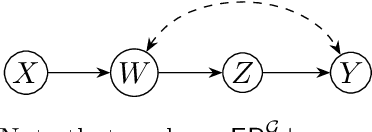
The aim of this paper is to make clear and precise the relationship between the Rubin causal model (RCM) and structural causal model (SCM) frameworks for causal inference. Adopting a neutral logical perspective, and drawing on previous work, we show what is required for an RCM to be representable by an SCM. A key result then shows that every RCM -- including those that violate algebraic principles implied by the SCM framework -- emerges as an abstraction of some representable RCM. Finally, we illustrate the power of this ameliorative perspective by pinpointing an important role for SCM principles in classic applications of RCMs; conversely, we offer a characterization of the algebraic constraints implied by a graph, helping to substantiate further comparisons between the two frameworks.

A Topological Perspective on Causal Inference

This paper presents a topological learning-theoretic perspective on causal inference by introducing a series of topologies defined on general spaces of structural causal models (SCMs). As an illustration of the framework we prove a topological causal hierarchy theorem, showing that substantive assumption-free causal inference is possible only in a meager set of SCMs. Thanks to a known correspondence between open sets in the weak topology and statistically verifiable hypotheses, our results show that inductive assumptions sufficient to license valid causal inferences are statistically unverifiable in principle. Similar to no-free-lunch theorems for statistical inference, the present results clarify the inevitability of substantial assumptions for causal inference. An additional benefit of our topological approach is that it easily accommodates SCMs with infinitely many variables. We finally suggest that the framework may be helpful for the positive project of exploring and assessing alternative causal-inductive assumptions.

Probabilistic Reasoning across the Causal Hierarchy

We propose a formalization of the three-tier causal hierarchy of association, intervention, and counterfactuals as a series of probabilistic logical languages. Our languages are of strictly increasing expressivity, the first capable of expressing quantitative probabilistic reasoning---including conditional independence and Bayesian inference---the second encoding do-calculus reasoning for causal effects, and the third capturing a fully expressive do-calculus for arbitrary counterfactual queries. We give a corresponding series of finitary axiomatizations complete over both structural causal models and probabilistic programs, and show that satisfiability and validity for each language are decidable in polynomial space.

On Open-Universe Causal Reasoning

We extend two kinds of causal models, structural equation models and simulation models, to infinite variable spaces. This enables a semantics for conditionals founded on a calculus of intervention, and axiomatization of causal reasoning for rich, expressive generative models---including those in which a causal representation exists only implicitly---in an open-universe setting. Further, we show that under suitable restrictions the two kinds of models are equivalent, perhaps surprisingly as their axiomatizations differ substantially in the general case. We give a series of complete axiomatizations in which the open-universe nature of the setting is seen to be essential.

Causal Modeling with Probabilistic Simulation Models

Recent authors have proposed analyzing conditional reasoning through a notion of intervention on a simulation program, and have found a sound and complete axiomatization of the logic of conditionals in this setting. Here we extend this setting to the case of probabilistic simulation models. We give a natural definition of probability on formulas of the conditional language, allowing for the expression of counterfactuals, and prove foundational results about this definition. We also find an axiomatization for reasoning about linear inequalities involving probabilities in this setting. We prove soundness, completeness, and NP-completeness of the satisfiability problem for this logic.

On the Conditional Logic of Simulation Models

We propose analyzing conditional reasoning by appeal to a notion of intervention on a simulation program, formalizing and subsuming a number of approaches to conditional thinking in the recent AI literature. Our main results include a series of axiomatizations, allowing comparison between this framework and existing frameworks (normality-ordering models, causal structural equation models), and a complexity result establishing NP-completeness of the satisfiability problem. Perhaps surprisingly, some of the basic logical principles common to all existing approaches are invalidated in our causal simulation approach. We suggest that this additional flexibility is important in modeling some intuitive examples.