Doros N. Theodorou
Developing Machine-Learned Potentials for Coarse-Grained Molecular Simulations: Challenges and Pitfalls
Sep 26, 2022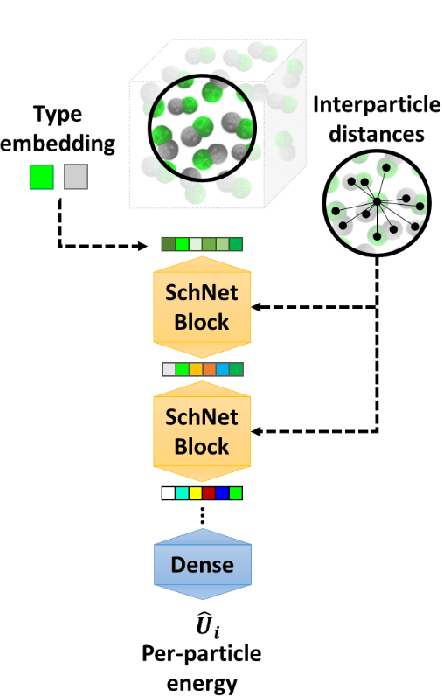
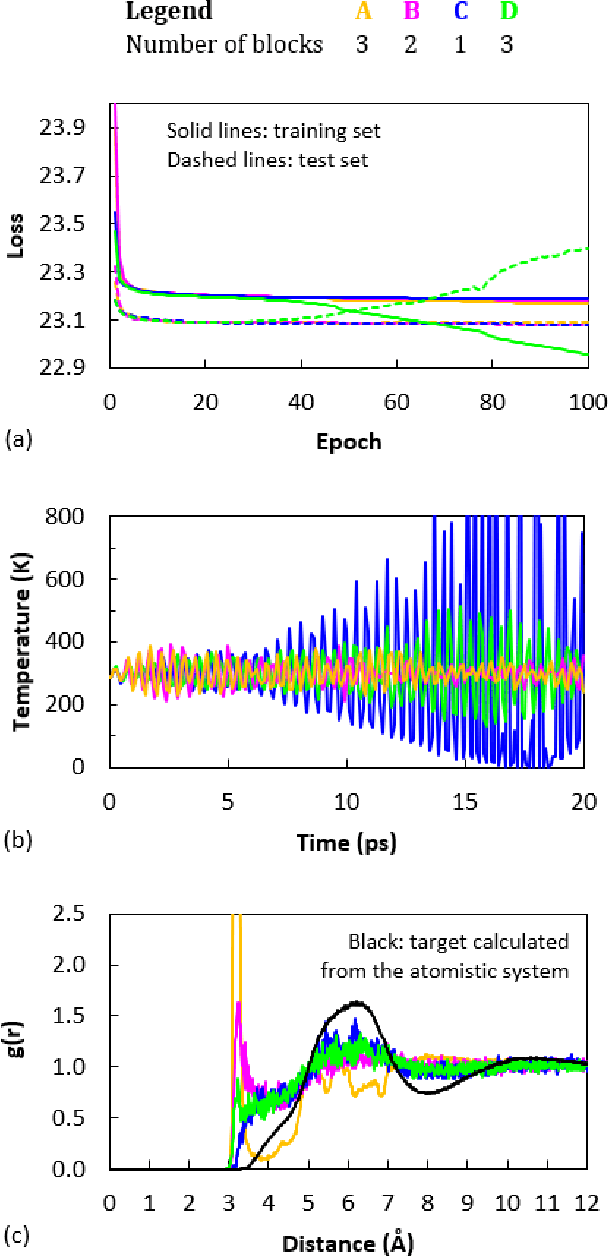
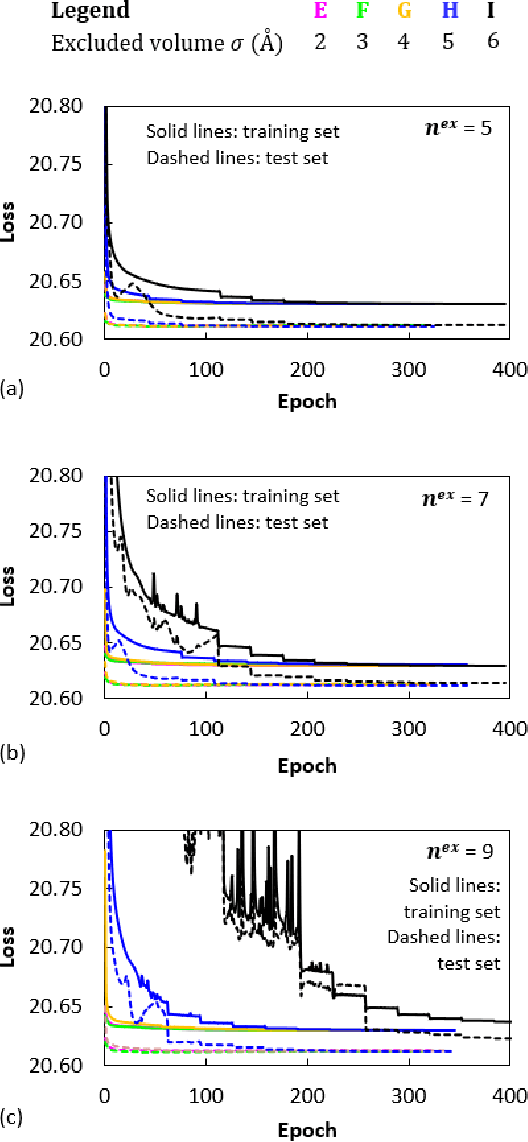
Abstract:Coarse graining (CG) enables the investigation of molecular properties for larger systems and at longer timescales than the ones attainable at the atomistic resolution. Machine learning techniques have been recently proposed to learn CG particle interactions, i.e. develop CG force fields. Graph representations of molecules and supervised training of a graph convolutional neural network architecture are used to learn the potential of mean force through a force matching scheme. In this work, the force acting on each CG particle is correlated to a learned representation of its local environment that goes under the name of SchNet, constructed via continuous filter convolutions. We explore the application of SchNet models to obtain a CG potential for liquid benzene, investigating the effect of model architecture and hyperparameters on the thermodynamic, dynamical, and structural properties of the simulated CG systems, reporting and discussing challenges encountered and future directions envisioned.
Investigation of Machine Learning-based Coarse-Grained Mapping Schemes for Organic Molecules
Sep 26, 2022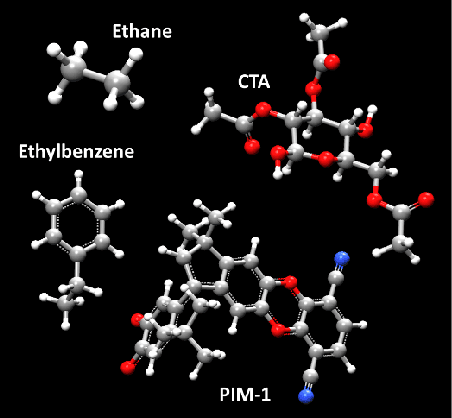
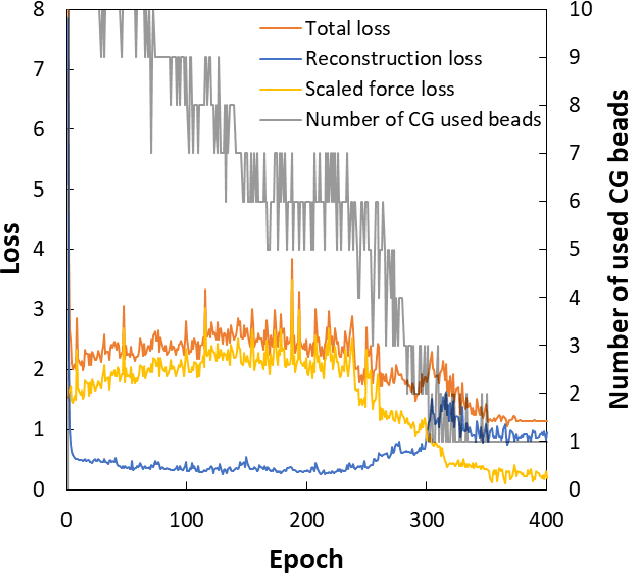
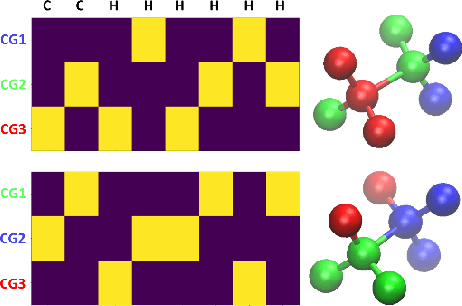
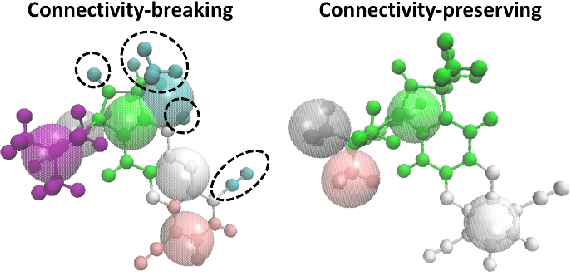
Abstract:Due to the wide range of timescales that are present in macromolecular systems, hierarchical multiscale strategies are necessary for their computational study. Coarse-graining (CG) allows to establish a link between different system resolutions and provides the backbone for the development of robust multiscale simulations and analyses. The CG mapping process is typically system- and application-specific, and it relies on chemical intuition. In this work, we explored the application of a Machine Learning strategy, based on Variational Autoencoders, for the development of suitable mapping schemes from the atomistic to the coarse-grained space of molecules with increasing chemical complexity. An extensive evaluation of the effect of the model hyperparameters on the training process and on the final output was performed, and an existing method was extended with the definition of different loss functions and the implementation of a selection criterion that ensures physical consistency of the output. The relationship between the input feature choice and the reconstruction accuracy was analyzed, supporting the need to introduce rotational invariance into the system. Strengths and limitations of the approach, both in the mapping and in the backmapping steps, are highlighted and critically discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge