Dynamic Memory Based Adaptive Optimization

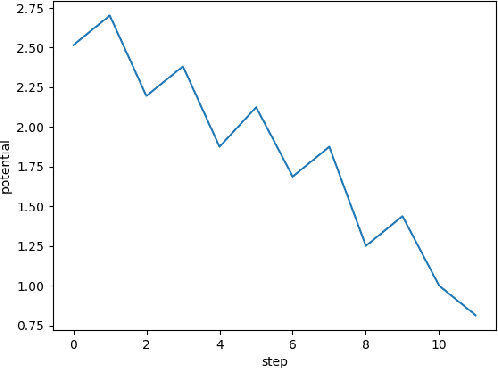
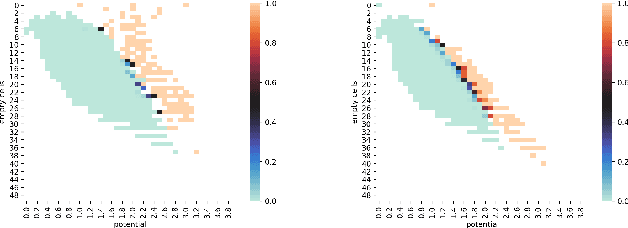
Define an optimizer as having memory $k$ if it stores $k$ dynamically changing vectors in the parameter space. Classical SGD has memory $0$, momentum SGD optimizer has $1$ and Adam optimizer has $2$. We address the following questions: How can optimizers make use of more memory units? What information should be stored in them? How to use them for the learning steps? As an approach to the last question, we introduce a general method called "Retrospective Learning Law Correction" or shortly RLLC. This method is designed to calculate a dynamically varying linear combination (called learning law) of memory units, which themselves may evolve arbitrarily. We demonstrate RLLC on optimizers whose memory units have linear update rules and small memory ($\leq 4$ memory units). Our experiments show that in a variety of standard problems, these optimizers outperform the above mentioned three classical optimizers. We conclude that RLLC is a promising framework for boosting the performance of known optimizers by adding more memory units and by making them more adaptive.

Towards solving the 7-in-a-row game

Our paper explores the game theoretic value of the 7-in-a-row game. We reduce the problem to solving a finite board game, which we target using Proof Number Search. We present a number of heuristic improvements to Proof Number Search and examine their effect within the context of this particular game. Although our paper does not solve the 7-in-a-row game, our experiments indicate that we have made significant progress towards it.