Reinforcement Learning in Conflicting Environments for Autonomous Vehicles

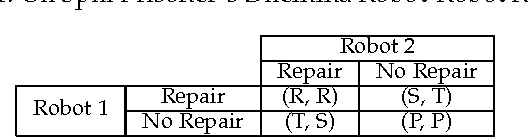
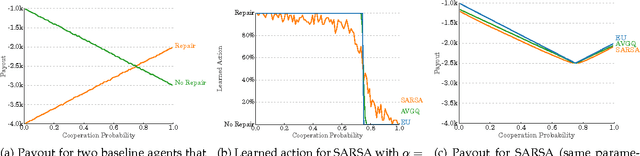
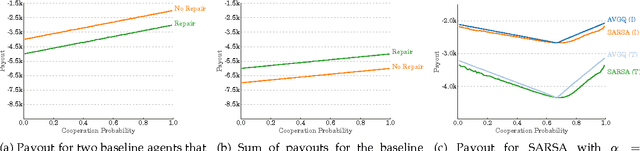
In this work, we investigate the application of Reinforcement Learning to two well known decision dilemmas, namely Newcomb's Problem and Prisoner's Dilemma. These problems are exemplary for dilemmas that autonomous agents are faced with when interacting with humans. Furthermore, we argue that a Newcomb-like formulation is more adequate in the human-machine interaction case and demonstrate empirically that the unmodified Reinforcement Learning algorithms end up with the well known maximum expected utility solution.

$\ell_1$ Regularized Gradient Temporal-Difference Learning

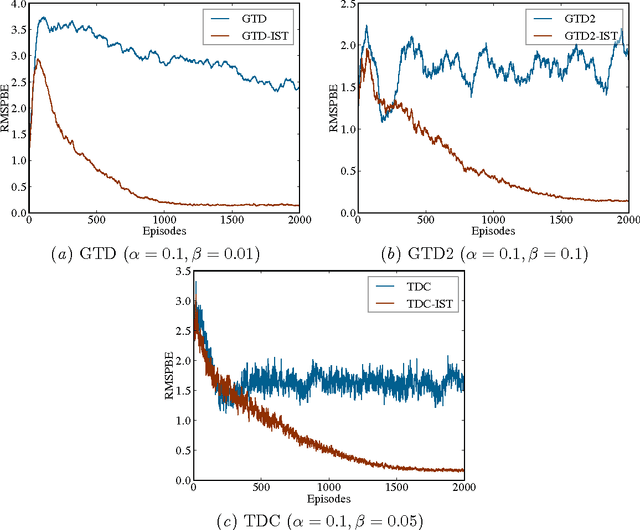
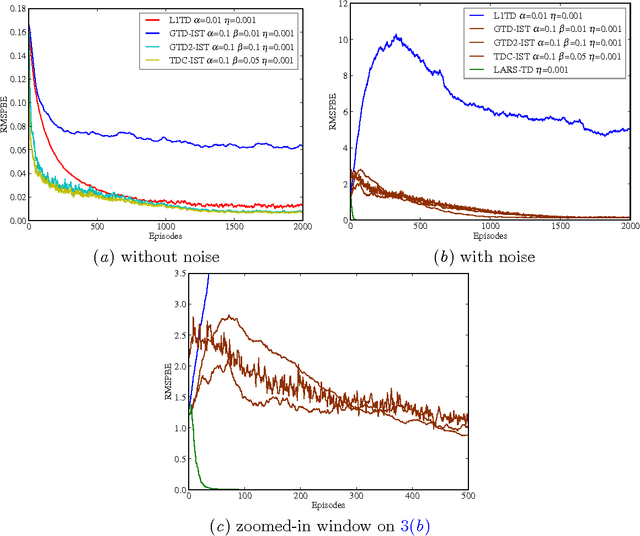
In this paper, we study the Temporal Difference (TD) learning with linear value function approximation. It is well known that most TD learning algorithms are unstable with linear function approximation and off-policy learning. Recent development of Gradient TD (GTD) algorithms has addressed this problem successfully. However, the success of GTD algorithms requires a set of well chosen features, which are not always available. When the number of features is huge, the GTD algorithms might face the problem of overfitting and being computationally expensive. To cope with this difficulty, regularization techniques, in particular $\ell_1$ regularization, have attracted significant attentions in developing TD learning algorithms. The present work combines the GTD algorithms with $\ell_1$ regularization. We propose a family of $\ell_1$ regularized GTD algorithms, which employ the well known soft thresholding operator. We investigate convergence properties of the proposed algorithms, and depict their performance with several numerical experiments.

Texture Retrieval via the Scattering Transform

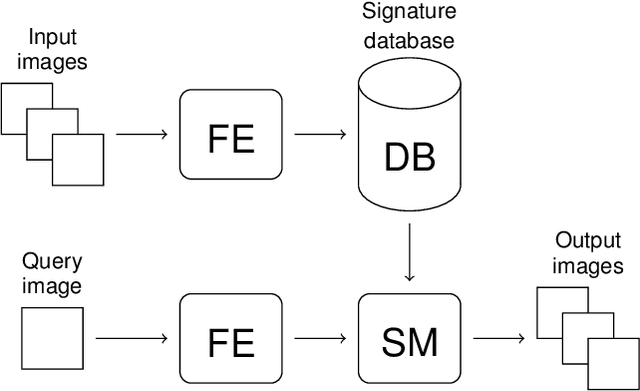
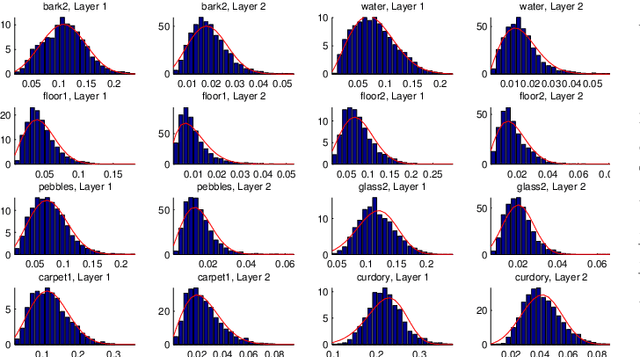
This work studies the problem of content-based image retrieval, specifically, texture retrieval. It focuses on feature extraction and similarity measure for texture images. Our approach employs a recently developed method, the so-called Scattering transform, for the process of feature extraction in texture retrieval. It shares a distinctive property of providing a robust representation, which is stable with respect to spatial deformations. Recent work has demonstrated its capability for texture classification, and hence as a promising candidate for the problem of texture retrieval. Moreover, we adopt a common approach of measuring the similarity of textures by comparing the subband histograms of a filterbank transform. To this end we derive a similarity measure based on the popular Bhattacharyya Kernel. Despite the popularity of describing histograms using parametrized probability density functions, such as the Generalized Gaussian Distribution, it is unfortunately not applicable for describing most of the Scattering transform subbands, due to the complex modulus performed on each one of them. In this work, we propose to use the Weibull distribution to model the Scattering subbands of descendant layers. Our numerical experiments demonstrated the effectiveness of the proposed approach, in comparison with several state of the arts.