The GECo algorithm for Graph Neural Networks Explanation

Graph Neural Networks (GNNs) are powerful models that can manage complex data sources and their interconnection links. One of GNNs' main drawbacks is their lack of interpretability, which limits their application in sensitive fields. In this paper, we introduce a new methodology involving graph communities to address the interpretability of graph classification problems. The proposed method, called GECo, exploits the idea that if a community is a subset of graph nodes densely connected, this property should play a role in graph classification. This is reasonable, especially if we consider the message-passing mechanism, which is the basic mechanism of GNNs. GECo analyzes the contribution to the classification result of the communities in the graph, building a mask that highlights graph-relevant structures. GECo is tested for Graph Convolutional Networks on six artificial and four real-world graph datasets and is compared to the main explainability methods such as PGMExplainer, PGExplainer, GNNExplainer, and SubgraphX using four different metrics. The obtained results outperform the other methods for artificial graph datasets and most real-world datasets.

From Specific to Generic Learned Sorted Set Dictionaries: A Theoretically Sound Paradigm Yelding Competitive Data Structural Boosters in Practice

This research concerns Learned Data Structures, a recent area that has emerged at the crossroad of Machine Learning and Classic Data Structures. It is methodologically important and with a high practical impact. We focus on Learned Indexes, i.e., Learned Sorted Set Dictionaries. The proposals available so far are specific in the sense that they can boost, indeed impressively, the time performance of Table Search Procedures with a sorted layout only, e.g., Binary Search. We propose a novel paradigm that, complementing known specialized ones, can produce Learned versions of any Sorted Set Dictionary, for instance, Balanced Binary Search Trees or Binary Search on layouts other that sorted, i.e., Eytzinger. Theoretically, based on it, we obtain several results of interest, such as (a) the first Learned Optimum Binary Search Forest, with mean access time bounded by the Entropy of the probability distribution of the accesses to the Dictionary; (b) the first Learned Sorted Set Dictionary that, in the Dynamic Case and in an amortized analysis setting, matches the same time bounds known for Classic Dictionaries. This latter under widely accepted assumptions regarding the size of the Universe. The experimental part, somewhat complex in terms of software development, clearly indicates the nonobvious finding that the generalization we propose can yield effective and competitive Learned Data Structural Booster, even with respect to specific benchmark models.

On the Suitability of Neural Networks as Building Blocks for The Design of Efficient Learned Indexes

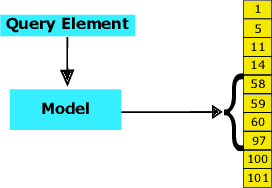
With the aim of obtaining time/space improvements in classic Data Structures, an emerging trend is to combine Machine Learning techniques with the ones proper of Data Structures. This new area goes under the name of Learned Data Structures. The motivation for its study is a perceived change of paradigm in Computer Architectures that would favour the use of Graphics Processing Units and Tensor Processing Units over conventional Central Processing Units. In turn, that would favour the use of Neural Networks as building blocks of Classic Data Structures. Indeed, Learned Bloom Filters, which are one of the main pillars of Learned Data Structures, make extensive use of Neural Networks to improve the performance of classic Filters. However, no use of Neural Networks is reported in the realm of Learned Indexes, which is another main pillar of that new area. In this contribution, we provide the first, and much needed, comparative experimental analysis regarding the use of Neural Networks as building blocks of Learned Indexes. The results reported here highlight the need for the design of very specialized Neural Networks tailored to Learned Indexes and it establishes a solid ground for those developments. Our findings, methodologically important, are of interest to both Scientists and Engineers working in Neural Networks Design and Implementation, in view also of the importance of the application areas involved, e.g., Computer Networks and Data Bases.

Standard Vs Uniform Binary Search and Their Variants in Learned Static Indexing: The Case of the Searching on Sorted Data Benchmarking Software Platform

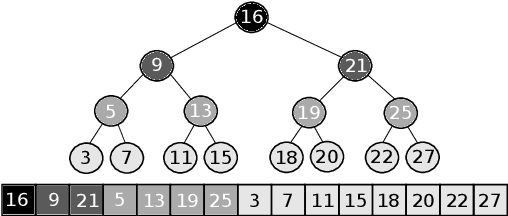
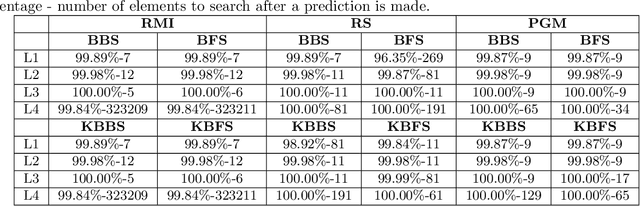
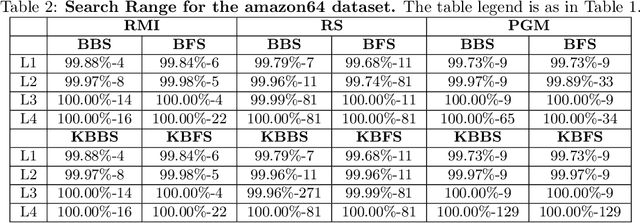
The Searching on Sorted Data ({\bf SOSD}, in short) is a highly engineered software platform for benchmarking Learned Indexes, those latter being a novel and quite effective proposal of how to search in a sorted table by combining Machine Learning techniques with classic Algorithms. In such a platform and in the related benchmarking experiments, following a natural and intuitive choice, the final search stage is performed via the Standard (textbook) Binary Search procedure. However, recent studies, that do not use Machine Learning predictions, indicate that Uniform Binary Search, streamlined to avoid \vir{branching} in the main loop, is superior in performance to its Standard counterpart when the table to be searched into is relatively small, e.g., fitting in L1 or L2 cache. Analogous results hold for k-ary Search, even on large tables. One would expect an analogous behaviour within Learned Indexes. Via a set of extensive experiments, coherent with the State of the Art, we show that for Learned Indexes, and as far as the {\bf SOSD} software is concerned, the use of the Standard routine (either Binary or k-ary Search) is superior to the Uniform one, across all the internal memory levels. This fact provides a quantitative justification of the natural choice made so far. Our experiments also indicate that Uniform Binary and k-ary Search can be advantageous to use in order to save space in Learned Indexes, while granting a good performance in time. Our findings are of methodological relevance for this novel and fast-growing area and informative to practitioners interested in using Learned Indexes in application domains, e.g., Data Bases and Search Engines.

Learned Sorted Table Search and Static Indexes in Small Space: Methodological and Practical Insights via an Experimental Study

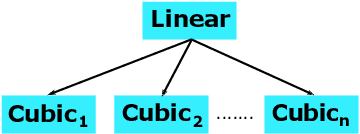
Sorted Table Search Procedures are the quintessential query-answering tool, still very useful, e.g, Search Engines (Google Chrome). Speeding them up, in small additional space with respect to the table being searched into, is still a quite significant achievement. Static Learned Indexes have been very successful in achieving such a speed-up, but leave open a major question: To what extent one can enjoy the speed-up of Learned Indexes while using constant or nearly constant additional space. By generalizing the experimental methodology of a recent benchmarking study on Learned Indexes, we shed light on this question, by considering two scenarios. The first, quite elementary, i.e., textbook code, and the second using advanced Learned Indexing algorithms and the supporting sophisticated software platforms. Although in both cases one would expect a positive answer, its achievement is not as simple as it seems. Indeed, our extensive set of experiments reveal a complex relationship between query time and model space. The findings regarding this relationship and the corresponding quantitative estimates, across memory levels, can be of interest to algorithm designers and of use to practitioners as well. As an essential part of our research, we introduce two new models that are of interest in their own right. The first is a constant space model that can be seen as a generalization of $k$-ary search, while the second is a synoptic {\bf RMI}, in which we can control model space usage.

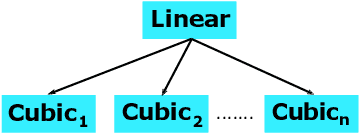
Learning from Data to Speed-up Sorted Table Search Procedures: Methodology and Practical Guidelines

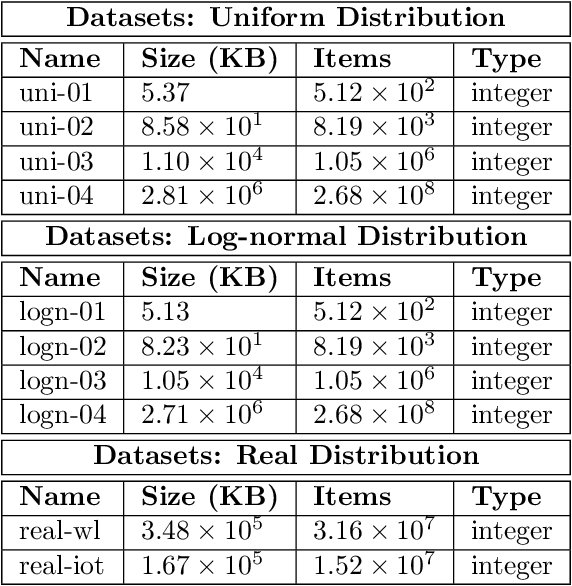
Sorted Table Search Procedures are the quintessential query-answering tool, with widespread usage that now includes also Web Applications, e.g, Search Engines (Google Chrome) and ad Bidding Systems (AppNexus). Speeding them up, at very little cost in space, is still a quite significant achievement. Here we study to what extend Machine Learning Techniques can contribute to obtain such a speed-up via a systematic experimental comparison of known efficient implementations of Sorted Table Search procedures, with different Data Layouts, and their Learned counterparts developed here. We characterize the scenarios in which those latter can be profitably used with respect to the former, accounting for both CPU and GPU computing. Our approach contributes also to the study of Learned Data Structures, a recent proposal to improve the time/space performance of fundamental Data Structures, e.g., B-trees, Hash Tables, Bloom Filters. Indeed, we also formalize an Algorithmic Paradigm of Learned Dichotomic Sorted Table Search procedures that naturally complements the Learned one proposed here and that characterizes most of the known Sorted Table Search Procedures as having a "learning phase" that approximates Simple Linear Regression.