Efficient Mixed Dimension Embeddings for Matrix Factorization

Despite the prominence of neural network approaches in the field of recommender systems, simple methods such as matrix factorization with quadratic loss are still used in industry for several reasons. These models can be trained with alternating least squares, which makes them easy to implement in a massively parallel manner, thus making it possible to utilize billions of events from real-world datasets. Large-scale recommender systems need to account for severe popularity skew in the distributions of users and items, so a lot of research is focused on implementing sparse, mixed dimension or shared embeddings to reduce both the number of parameters and overfitting on rare users and items. In this paper we propose two matrix factorization models with mixed dimension embeddings, which can be optimized in a massively parallel fashion using the alternating least squares approach.

Reinforcement Learning Enhanced Quantum-inspired Algorithm for Combinatorial Optimization

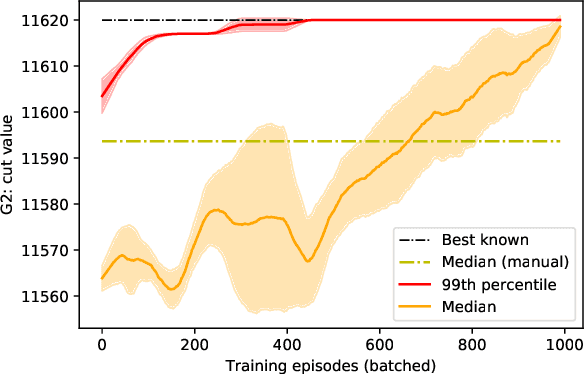
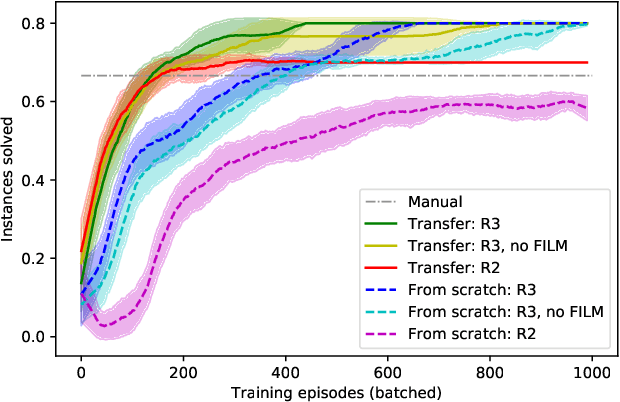
Quantum hardware and quantum-inspired algorithms are becoming increasingly popular for combinatorial optimization. However, these algorithms may require careful hyperparameter tuning for each problem instance. We use a reinforcement learning agent in conjunction with a quantum-inspired algorithm to solve the Ising energy minimization problem, which is equivalent to the Maximum Cut problem. The agent controls the algorithm by tuning one of its parameters with the goal of improving recently seen solutions. We propose a new Rescaled Ranked Reward (R3) method that enables stable single-player version of self-play training that helps the agent to escape local optima. The training on any problem instance can be accelerated by applying transfer learning from an agent trained on randomly generated problems. Our approach allows sampling high-quality solutions to the Ising problem with high probability and outperforms both baseline heuristics and a black-box hyperparameter optimization approach.