Tight FPT Approximation for Constrained k-Center and k-Supplier

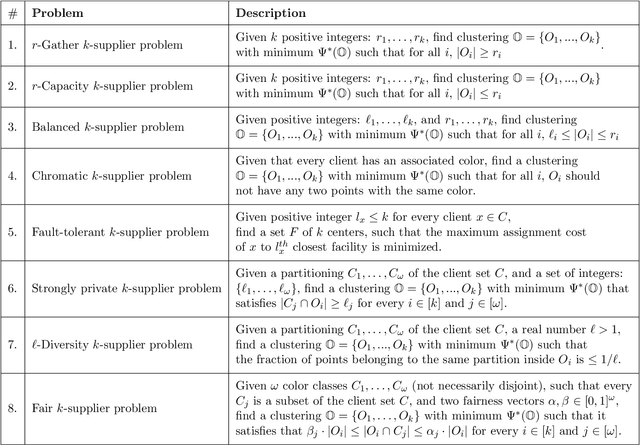
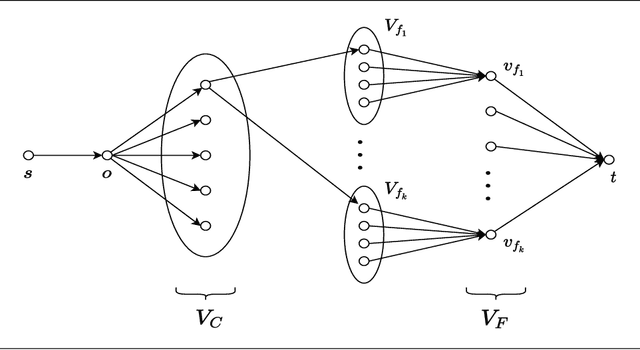
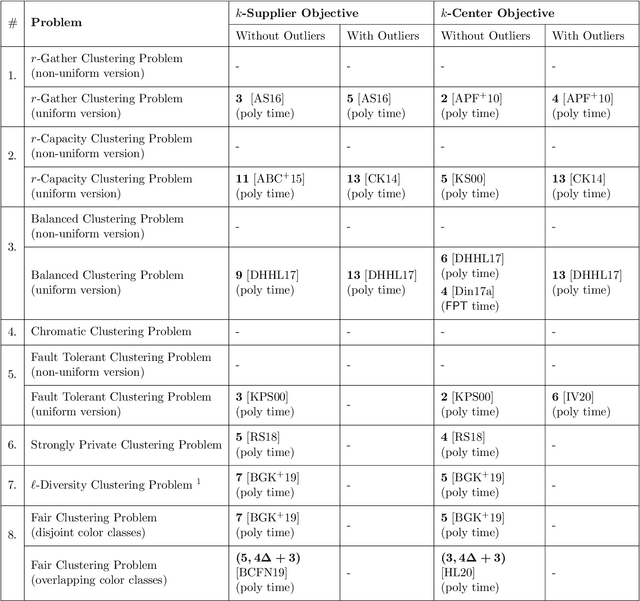
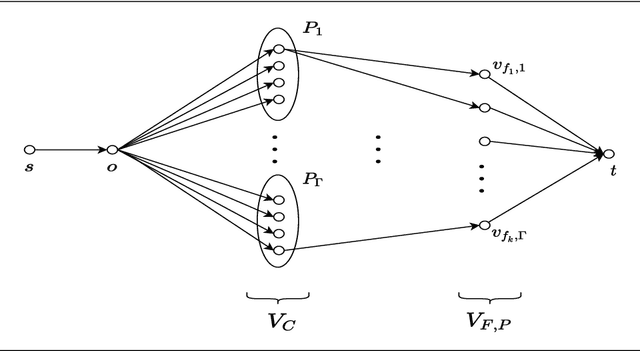
In this work, we study a range of constrained versions of the $k$-supplier and $k$-center problems such as: capacitated, fault-tolerant, fair, etc. These problems fall under a broad framework of constrained clustering. A unified framework for constrained clustering was proposed by Ding and Xu [SODA 2015] in context of the $k$-median and $k$-means objectives. In this work, we extend this framework to the $k$-supplier and $k$-center objectives. This unified framework allows us to obtain results simultaneously for the following constrained versions of the $k$-supplier problem: $r$-gather, $r$-capacity, balanced, chromatic, fault-tolerant, strongly private, $\ell$-diversity, and fair $k$-supplier problems, with and without outliers. We obtain the following results: We give $3$ and $2$ approximation algorithms for the constrained $k$-supplier and $k$-center problems, respectively, with $\mathsf{FPT}$ running time $k^{O(k)} \cdot n^{O(1)}$, where $n = |C \cup L|$. Moreover, these approximation guarantees are tight; that is, for any constant $\epsilon>0$, no algorithm can achieve $(3-\epsilon)$ and $(2-\epsilon)$ approximation guarantees for the constrained $k$-supplier and $k$-center problems in $\mathsf{FPT}$ time, assuming $\mathsf{FPT} \neq \mathsf{W}[2]$. Furthermore, we study these constrained problems in outlier setting. Our algorithm gives $3$ and $2$ approximation guarantees for the constrained outlier $k$-supplier and $k$-center problems, respectively, with $\mathsf{FPT}$ running time $(k+m)^{O(k)} \cdot n^{O(1)}$, where $n = |C \cup L|$ and $m$ is the number of outliers.

FPT Approximation for Socially Fair Clustering

In this work, we study the socially fair $k$-median/$k$-means problem. We are given a set of points $P$ in a metric space $\mathcal{X}$ with a distance function $d(.,.)$. There are $\ell$ groups: $P_1,\dotsc,P_{\ell} \subseteq P$. We are also given a set $F$ of feasible centers in $\mathcal{X}$. The goal of the socially fair $k$-median problem is to find a set $C \subseteq F$ of $k$ centers that minimizes the maximum average cost over all the groups. That is, find $C$ that minimizes the objective function $\Phi(C,P) \equiv \max_{j} \sum_{x \in P_j} d(C,x)/|P_j|$, where $d(C,x)$ is the distance of $x$ to the closest center in $C$. The socially fair $k$-means problem is defined similarly by using squared distances, i.e., $d^{2}(.,.)$ instead of $d(.,.)$. In this work, we design $(5+\varepsilon)$ and $(33 + \varepsilon)$ approximation algorithms for the socially fair $k$-median and $k$-means problems, respectively. For the parameters: $k$ and $\ell$, the algorithms have an FPT (fixed parameter tractable) running time of $f(k,\ell,\varepsilon) \cdot n$ for $f(k,\ell,\varepsilon) = 2^{{O}(k \, \ell/\varepsilon)}$ and $n = |P \cup F|$. We also study a special case of the problem where the centers are allowed to be chosen from the point set $P$, i.e., $P \subseteq F$. For this special case, our algorithms give better approximation guarantees of $(4+\varepsilon)$ and $(18+\varepsilon)$ for the socially fair $k$-median and $k$-means problems, respectively. Furthermore, we convert these algorithms to constant pass log-space streaming algorithms. Lastly, we show FPT hardness of approximation results for the problem with a small gap between our upper and lower bounds.

Hardness of Approximation of Euclidean $k$-Median

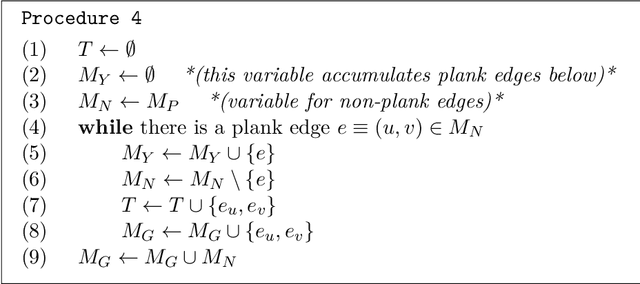
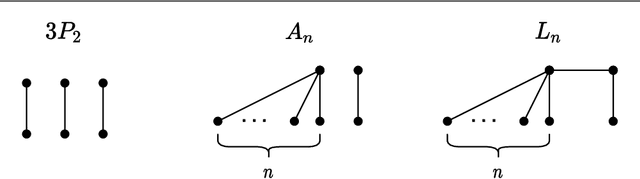
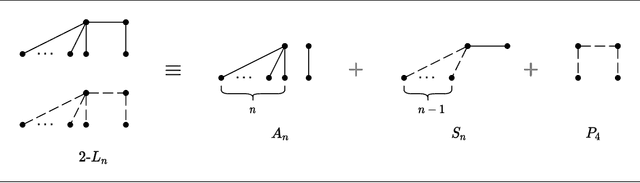
The Euclidean $k$-median problem is defined in the following manner: given a set $\mathcal{X}$ of $n$ points in $\mathbb{R}^{d}$, and an integer $k$, find a set $C \subset \mathbb{R}^{d}$ of $k$ points (called centers) such that the cost function $\Phi(C,\mathcal{X}) \equiv \sum_{x \in \mathcal{X}} \min_{c \in C} \|x-c\|_{2}$ is minimized. The Euclidean $k$-means problem is defined similarly by replacing the distance with squared distance in the cost function. Various hardness of approximation results are known for the Euclidean $k$-means problem. However, no hardness of approximation results were known for the Euclidean $k$-median problem. In this work, assuming the unique games conjecture (UGC), we provide the first hardness of approximation result for the Euclidean $k$-median problem. Furthermore, we study the hardness of approximation for the Euclidean $k$-means/$k$-median problems in the bi-criteria setting where an algorithm is allowed to choose more than $k$ centers. That is, bi-criteria approximation algorithms are allowed to output $\beta k$ centers (for constant $\beta>1$) and the approximation ratio is computed with respect to the optimal $k$-means/$k$-median cost. In this setting, we show the first hardness of approximation result for the Euclidean $k$-median problem for any $\beta < 1.015$, assuming UGC. We also show a similar bi-criteria hardness of approximation result for the Euclidean $k$-means problem with a stronger bound of $\beta < 1.28$, again assuming UGC.