Hardness of Approximation of Euclidean $k$-Median
Paper and Code
Nov 09, 2020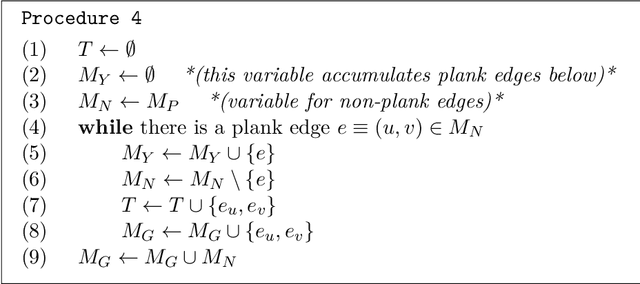

The Euclidean $k$-median problem is defined in the following manner: given a set $\mathcal{X}$ of $n$ points in $\mathbb{R}^{d}$, and an integer $k$, find a set $C \subset \mathbb{R}^{d}$ of $k$ points (called centers) such that the cost function $\Phi(C,\mathcal{X}) \equiv \sum_{x \in \mathcal{X}} \min_{c \in C} \|x-c\|_{2}$ is minimized. The Euclidean $k$-means problem is defined similarly by replacing the distance with squared distance in the cost function. Various hardness of approximation results are known for the Euclidean $k$-means problem. However, no hardness of approximation results were known for the Euclidean $k$-median problem. In this work, assuming the unique games conjecture (UGC), we provide the first hardness of approximation result for the Euclidean $k$-median problem. Furthermore, we study the hardness of approximation for the Euclidean $k$-means/$k$-median problems in the bi-criteria setting where an algorithm is allowed to choose more than $k$ centers. That is, bi-criteria approximation algorithms are allowed to output $\beta k$ centers (for constant $\beta>1$) and the approximation ratio is computed with respect to the optimal $k$-means/$k$-median cost. In this setting, we show the first hardness of approximation result for the Euclidean $k$-median problem for any $\beta < 1.015$, assuming UGC. We also show a similar bi-criteria hardness of approximation result for the Euclidean $k$-means problem with a stronger bound of $\beta < 1.28$, again assuming UGC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge